题目内容
若a=20.5,b=logπ3,c=log2(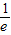 ) 则( )
) 则( )A.a>b>c
B.b>a>c
C.c>a>b
D.b>c>a
【答案】分析:根据指数函数与对数函数的单调性质将a,b,c分别与1与0比较即可.
解答:解:∵a=20.5>2=1,
0=logπ1<b=logπ3<logππ=1,
c=log2(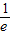 )<log21=0,
)<log21=0,
∴a>b>c.
故选A.
点评:本题考查对数的运算性质,考查指数函数与对数函数的单调性,属于基础题.
解答:解:∵a=20.5>2=1,
0=logπ1<b=logπ3<logππ=1,
c=log2(
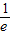 )<log21=0,
)<log21=0,∴a>b>c.
故选A.
点评:本题考查对数的运算性质,考查指数函数与对数函数的单调性,属于基础题.

练习册系列答案
相关题目
若a=20.5,b=logπ3,c=log2sin
,则( )
| 2π |
| 5 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |