题目内容
过双曲线
-
=1(a>0,b>0)的右焦点作直线l,交双曲线于A,B两点,且|AB|=2a,若这样的直线l有且只有一条,则双曲线离心率的取值范围是
| x2 |
| a2 |
| y2 |
| b2 |
e>
| 2 |
e>
.| 2 |
分析:若过点F且|AB|=2a,若这样的直线l有且只有一条,利用双曲线的对称性,则该直线的必定垂直于x轴.根据这个结论可以求出双曲线离心率的取值范围.
解答: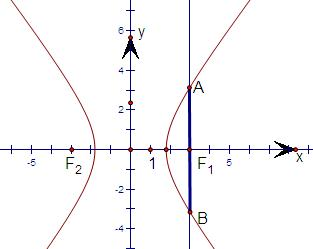 解:已知双曲线
解:已知双曲线
-
=1(a>0,b>0)的右焦点为F,
若过点F且|AB|=2a,若这样的直线l有且只有一条,
则此直线必为X轴,且两点都在右支上的弦都大于2a
据双曲线的对称性,作出垂直于x轴直线,其对应弦是图中的线段AB,只需要AB>2a即可.
由于|AB|=2|AF1|=2
=
令|AB|>2a,
∴
>2a,
即
>a,
>
,
则双曲线离心率的取值范围是e>
故答案为:e>
.
 解:已知双曲线
解:已知双曲线 | x2 |
| a2 |
| y2 |
| b2 |
若过点F且|AB|=2a,若这样的直线l有且只有一条,
则此直线必为X轴,且两点都在右支上的弦都大于2a
据双曲线的对称性,作出垂直于x轴直线,其对应弦是图中的线段AB,只需要AB>2a即可.
由于|AB|=2|AF1|=2
b 2(
|
| 2b 2 |
| a |
令|AB|>2a,
∴
| 2b 2 |
| a |
即
| c 2-a 2 |
| a |
| c |
| a |
| 2 |
则双曲线离心率的取值范围是e>
| 2 |
故答案为:e>
| 2 |
点评:本题考查双曲线的性质及其应用,解题时要注意挖掘隐含条件.

练习册系列答案
相关题目
过双曲线
-
=1的左焦点F作⊙O:x2+y2=a2的两条切线,记切点为A,B,双曲线左顶点为C,若∠ACB=120°,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|