题目内容
已知α+2β= ,α和β为锐角;
,α和β为锐角;
(1)若tan(α+β)=2+ ;求β;
;求β;
(2)若tanβ=(2- )cot
)cot ,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由.
,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由.
解:(1)因为α+2β= ,
,
∴tanβ=tan[(α+2β)-(α+β)]=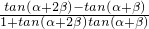 =
= =
=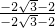 =1
=1
由β为锐角,得到β= .
.
(2)由α+2β= 得
得 +β=
+β= ,
,
∴tan( +β)=
+β)=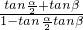 =tan
=tan =
= ,
,
∵tanβ=(2- )cot
)cot 即tan
即tan tanβ=2-
tanβ=2-
∴tan +tanβ=3-
+tanβ=3- ,
,
于是tan 和tanβ是一元二次方程x2-(3-
和tanβ是一元二次方程x2-(3- )x+2-
)x+2- =0的两根,
=0的两根,
解得x1=1,x2=2- .
.
若tan =1,则α=90°与0<α<90°矛盾,舍去;
=1,则α=90°与0<α<90°矛盾,舍去;
∴tan =2-
=2- ,tanβ=1,
,tanβ=1,
∴α=30°,β=45°,
故满足条件的α和β存在,且α=30°,β=45°.
分析:(1)根据β=[(α+2β)-(α+β)],然后利用两角差的正切函数公式对等式两边取正切,根据tan(α+β)=2+ 和α+2β=
和α+2β= 化简得到tanβ的值,根据特殊角的三角函数值求出β即可;
化简得到tanβ的值,根据特殊角的三角函数值求出β即可;
(2)由α+2β= 两边除以2得到
两边除以2得到 +β=
+β= ,两边去正切值得到正切之和和正切之积的关系,然后再根据tanβ=(2-
,两边去正切值得到正切之和和正切之积的关系,然后再根据tanβ=(2- )cot
)cot 得到正切之和,正切之积的值,利用根与系数的关系写出一个方程,求出方程的解,利用特殊角的三角函数值求出α和β,故存在这样的角度满足条件.
得到正切之和,正切之积的值,利用根与系数的关系写出一个方程,求出方程的解,利用特殊角的三角函数值求出α和β,故存在这样的角度满足条件.
点评:此题把三角函数和一元二次方程综合在一起,考查学生灵活运用角的变换,灵活运用两角差的正切函数的公式化简求值.
 ,
,∴tanβ=tan[(α+2β)-(α+β)]=
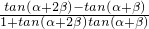 =
= =
=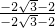 =1
=1由β为锐角,得到β=
 .
.(2)由α+2β=
 得
得 +β=
+β= ,
,∴tan(
 +β)=
+β)=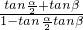 =tan
=tan =
= ,
,∵tanβ=(2-
 )cot
)cot 即tan
即tan tanβ=2-
tanβ=2-
∴tan
 +tanβ=3-
+tanβ=3- ,
,于是tan
 和tanβ是一元二次方程x2-(3-
和tanβ是一元二次方程x2-(3- )x+2-
)x+2- =0的两根,
=0的两根,解得x1=1,x2=2-
 .
.若tan
 =1,则α=90°与0<α<90°矛盾,舍去;
=1,则α=90°与0<α<90°矛盾,舍去;∴tan
 =2-
=2- ,tanβ=1,
,tanβ=1,∴α=30°,β=45°,
故满足条件的α和β存在,且α=30°,β=45°.
分析:(1)根据β=[(α+2β)-(α+β)],然后利用两角差的正切函数公式对等式两边取正切,根据tan(α+β)=2+
 和α+2β=
和α+2β= 化简得到tanβ的值,根据特殊角的三角函数值求出β即可;
化简得到tanβ的值,根据特殊角的三角函数值求出β即可;(2)由α+2β=
 两边除以2得到
两边除以2得到 +β=
+β= ,两边去正切值得到正切之和和正切之积的关系,然后再根据tanβ=(2-
,两边去正切值得到正切之和和正切之积的关系,然后再根据tanβ=(2- )cot
)cot 得到正切之和,正切之积的值,利用根与系数的关系写出一个方程,求出方程的解,利用特殊角的三角函数值求出α和β,故存在这样的角度满足条件.
得到正切之和,正切之积的值,利用根与系数的关系写出一个方程,求出方程的解,利用特殊角的三角函数值求出α和β,故存在这样的角度满足条件.点评:此题把三角函数和一元二次方程综合在一起,考查学生灵活运用角的变换,灵活运用两角差的正切函数的公式化简求值.

练习册系列答案
相关题目
 是1-a和1+a的等比中项,则a+4b的取值范围是 .
是1-a和1+a的等比中项,则a+4b的取值范围是 . 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
) 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
) 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
) 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
)