题目内容
【题目】等轴双曲线C的中心在原点，焦点在x轴上，双曲线C与抛物线y2=16x的准线交于A，B两点，|AB|=4 
，则双曲线C的实轴长为（ ）
A.
B.2
C.4
D.4
【答案】D
【解析】解：设等轴双曲线C的方程为x2﹣y2=λ．（λ＞0），① ∵抛物线y2=16x，2p=16，p=8，∴ 
=4．
∴抛物线的准线方程为x=﹣4．
设等轴双曲线与抛物线的准线x=﹣4的两个交点A（﹣4，y），B（﹣4，﹣y）（y＞0），
则|AB|=|y﹣（﹣y）|=2y=4 
，∴y=2 ．
将x=﹣4，y=2 代入①，得（﹣4）2﹣（2 ）2=λ，∴λ=8
∴等轴双曲线C的方程为x2﹣y2=8，即 
∴a= 
，C的实轴长为2a=4 ．
故选：D
练习册系列答案
相关题目
【题目】已知{an}是等比数列，满足a2=6，a3=﹣18，数列{bn}满足b1=2，且{2bn+an}是公差为2的等差数列．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）求数列{bn}的前n项和．
【题目】某地区2007年至2013年农村居民家庭人均纯收入y（单位：千元）的数据如表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为： 
= 
， 
= 
﹣ 
．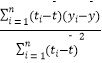