题目内容
已知等差数列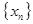 ,
,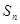 是
是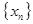 的前
的前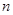 项和,且
项和,且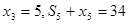 .
.
(1)求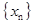 的通项公式;
的通项公式;
(2)设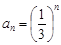 ,
,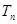 是
是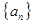 的前n项和,是否存在正数
的前n项和,是否存在正数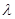 ,对任意正整数
,对任意正整数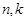 ,不等式
,不等式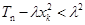 恒成立?若存在,求
恒成立?若存在,求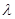 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(3)判断方程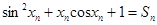 是否有解,说明理由;
是否有解,说明理由;
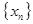 ,
,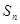 是
是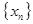 的前
的前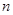 项和,且
项和,且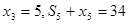 .
.(1)求
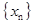 的通项公式;
的通项公式;(2)设
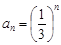 ,
,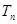 是
是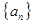 的前n项和,是否存在正数
的前n项和,是否存在正数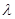 ,对任意正整数
,对任意正整数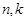 ,不等式
,不等式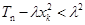 恒成立?若存在,求
恒成立?若存在,求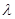 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.(3)判断方程
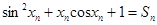 是否有解,说明理由;
是否有解,说明理由;(1)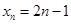 ;(2)
;(2)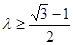 ;(3)无解。
;(3)无解。
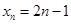 ;(2)
;(2)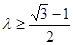 ;(3)无解。
;(3)无解。试题分析:(1)由
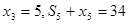 ,
,所以
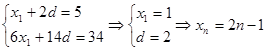
(2) 由
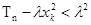 恒成立,则
恒成立,则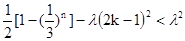 恒成立
恒成立即
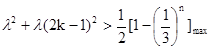
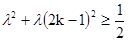 ,又
,又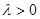 所以
所以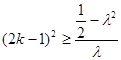 [
[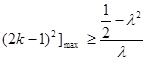 所以
所以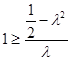 即
即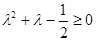 故
故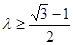
(3)
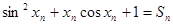 , 由于
, 由于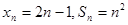 ,
,则方程为:

①
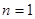 时,
时,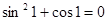 无解②
无解② 时,
时,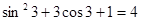 所以
所以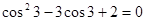 所以
所以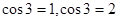 无解
无解 ③
 时,
时,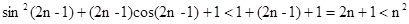
所以
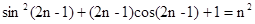 无解综上所述,对于一切正整数原方程都无解.
无解综上所述,对于一切正整数原方程都无解.点评:本题考查数列与不等式的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化。此题难度较大。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
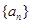 共有
共有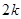 项(整数
项(整数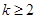 ),首项
),首项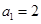 ,设该数列的前
,设该数列的前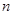 项和为
项和为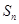 ,且
,且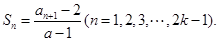 其中常数
其中常数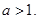 ⑴求
⑴求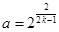 ,数列
,数列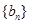 满足
满足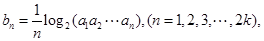
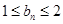 ;
;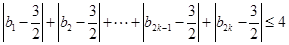 ,求
,求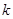 的最大值.
的最大值.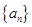 中,
中,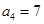 ,且
,且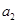 、
、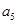 、
、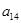 成等比数列.
成等比数列.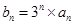 ,求数列
,求数列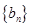 的前
的前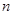 项的和
项的和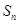 .
.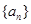 的前
的前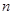 项和为
项和为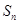 ,若
,若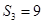 ,
,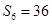 ,则
,则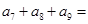 _____.
_____.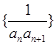 的前100项和为( )
的前100项和为( )



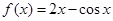 ,
,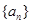 是公差为
是公差为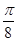 的等差数列,
的等差数列,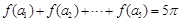 ,则
,则 .
.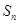 .已知
.已知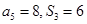 ,则
,则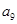 = ( )
= ( )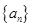 是等差数列,且
是等差数列,且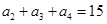 ,则这个数列的前5项和
,则这个数列的前5项和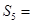 ___________
___________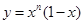 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为 ,则
,则 的前n项和是 .
的前n项和是 .