题目内容
18.设F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点,过F做双曲线一条渐近线的垂线与两条渐近线交于P,Q,若$\overline{FP}$=4$\overline{FQ}$,则双曲线的离心率是$\frac{2\sqrt{6}}{3}$.分析 设F(-c,0),过F作双曲线一条渐近线的垂线方程为y=$\frac{a}{b}$(x+c),与两条渐近线方程联立,求出P,Q的横坐标,利用$\overline{FP}$=4$\overline{FQ}$,建立方程,即可求出双曲线的离心率.
解答 解:设F(-c,0),过F作双曲线一条渐近线的垂线方程为y=$\frac{a}{b}$(x+c)
与y=-$\frac{a}{b}$x,联立可得x=-$\frac{{a}^{2}}{c}$;与y=$\frac{a}{b}$x联立可得x=$\frac{{a}^{2}c}{{b}^{2}-{a}^{2}}$,
∵$\overline{FP}$=4$\overline{FQ}$,
∴$\frac{{a}^{2}c}{{b}^{2}-{a}^{2}}$+c=4(-$\frac{{a}^{2}}{c}$+c),
∴a2c2=(c2-2a2)(3c2-4a2),
∴3e4-11e2+8=0,
∵e>1,∴e2=$\frac{8}{3}$
∴e=$\frac{2\sqrt{6}}{3}$.
故答案为:$\frac{2\sqrt{6}}{3}$.
点评 本题考查双曲线的性质,考查向量知识的运用,确定a,c的关系是关键.

练习册系列答案
相关题目
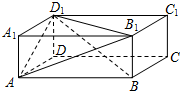 如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3.
如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3. 如图,过圆O外一点P分别作圆O的切线PA和割线PBC,其中A为切点,过点A作
如图,过圆O外一点P分别作圆O的切线PA和割线PBC,其中A为切点,过点A作 已知:在四棱锥P-ABCD中,PD⊥平面ABCD,PD=CD=BC=2AD,AD∥BC,∠BCD=90°
已知:在四棱锥P-ABCD中,PD⊥平面ABCD,PD=CD=BC=2AD,AD∥BC,∠BCD=90° 如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.
如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.