题目内容
【题目】已知函数y= 
sin（ωx+ 
）（ω＞0）． 
（1）若ω= ，求函数的单调增区间和对称中心；
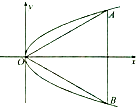
（2）函数的图象上有如图所示的A，B，C三点，且满足AB⊥BC． ①求ω的值；
②求函数在x∈[0，2）上的最大值，并求此时x的值．
【答案】
（1）解：ω= 
时，函数y= 
sin（ x+ ），
令﹣ 
+2kπ≤ x+ ≤ +2kπ，k∈Z，
解得：﹣3+8k≤x≤1+8k，k∈Z，
∴函数y的单调增区间为[﹣3+8k，1+8k]，（k∈Z）
令 x+ =kπ，k∈Z，
解得x=﹣1+4k，k∈Z，
∴函数y的对称中心为（﹣1+4k，0），（k∈Z）；
（2）解：①由图知：点B是函数图象的最高点，设B（xB， ），
设函数最小正周期为T，则A（xB﹣ 
，0），C（xB+ 
，0）；
∴ 
=（ ， ），
=（ ，﹣ ），
由 ⊥ ，得 = 
T2﹣3=0，
解得：T=4，
∴ω= 
= 
；
②由x∈[0，2]得 x+ ∈[ ， 
]，
∴sin（ x+ ）∈[﹣ 
，1]，
∴函数y在[0，2]上的最大值为 ，
此时 x+ = +2kπ，k∈Z，
则x= 
4k，k∈Z；
又x∈[0，2]，∴x= 
【解析】（1）ω= 
时求出函数y的单调增区间和对称中心；（2）①由图知B是函数图象的最高点，设出点B的坐标和最小正周期，表示出点A、C的坐标，利用坐标表示向量 
、 
，根据数量积求出T、ω的值；②由x的取值范围求出函数y的最大值，计算对应的x值．
【考点精析】根据题目的已知条件，利用正弦函数的单调性和三角函数的最值的相关知识可以得到问题的答案，需要掌握正弦函数的单调性：在
上是增函数；在
上是减函数；函数
，当
时，取得最小值为
；当
时，取得最大值为
，则
，
，
．
