题目内容
【题目】设数列![]() 的首项为
的首项为![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,均有
,均有![]() (
(![]() 是常数且
是常数且![]() )成立,则称数列
)成立,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为“
为“![]() 数列”,求数列
数列”,求数列![]() 的通项公式;
的通项公式;
(2)是否存在数列![]() 既是“
既是“![]() 数列”,也是“
数列”,也是“![]() 数列”?若存在,求出符合条件的数列
数列”?若存在,求出符合条件的数列![]() 的通项公式及对应的
的通项公式及对应的![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若数列![]() 为“
为“![]() 数列”,
数列”, ![]() ,设
,设![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ;(2)不存在;(3)证明见解析.
;(2)不存在;(3)证明见解析.
【解析】试题分析:
(1)由题意得![]() ,故
,故![]() ,两式相减可得
,两式相减可得![]() ,在此基础上可得数列
,在此基础上可得数列![]() 为等比数列,从而可得通项公式.(2)利用反证法可得不存在这样的数列
为等比数列,从而可得通项公式.(2)利用反证法可得不存在这样的数列![]() 既是“
既是“![]() 数列”,也是“
数列”,也是“![]() 数列”.(3)由数列
数列”.(3)由数列![]() 为“
为“![]() 数列”,可得到
数列”,可得到![]() 对任意正整数
对任意正整数![]() 恒成立,于是可得
恒成立,于是可得![]() ,然后根据错位相减法求得
,然后根据错位相减法求得![]()
![]() ,故得
,故得![]() ,故
,故![]() ,即
,即![]() ,即结论成立.
,即结论成立.
试题解析:
(1)因为数列![]() 为“
为“![]() 数列”,
数列”,
则![]()
故![]() ,
,
两式相减得: ![]() ,
,
又![]() 时,
时, ![]() ,
,
所以![]() ,
,
故![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() (常数),
(常数),
故数列![]() 为等比数列,其通项公式为
为等比数列,其通项公式为![]() .
.
(2)假设存在这样的数列![]() ,则有
,则有![]() ,故有
,故有![]()
两式相减得: ![]() ,
,
故有![]() ,
,
同理由![]() 是“
是“![]() 数列”可得
数列”可得![]() ,
,
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
所以![]() ,
,
即![]() ,
,
又![]() ,
,
即![]() ,
,
两者矛盾,故不存在这样的数列![]() 既是“
既是“![]() 数列”,也是“
数列”,也是“![]() 数列”.
数列”.
(3)因为数列![]() 为“
为“![]() 数列”,
数列”,
所以![]() ,
,
所以![]() ,
,
故有, ![]() ,
,
又![]() 时,
时, ![]() ,
,
故![]() ,满足
,满足![]() ,
,
所以![]() 对任意正整数
对任意正整数![]() 恒成立,数列的前几项为:
恒成立,数列的前几项为: ![]() .
.
故![]() ,
,
所以![]() ,
,
两式相减得 ![]()
![]() ,
,
显然![]() ,
,
故![]() ,
,
即![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
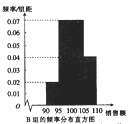
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
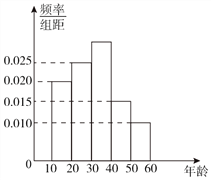
【题目】2017年是内蒙古自治区成立70周年.某市旅游文化局为了庆祝内蒙古自治区成立70周年,举办了第十三届成吉思汗旅游文化周.为了了解该市关注“旅游文化周”居民的年龄段分布,随机抽取了![]() 名年龄在
名年龄在![]() 且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
年龄 |
|
|
|
单人促销价格(单位:元) |
|
|
|
(Ⅰ)根据频率分布直方图,估计该市被抽取市民的年龄的平均数;
(Ⅱ)某旅行社针对“旅游文化周”开展不同年龄段的旅游促销活动,各年龄段的促销价位如表所示.已知该旅行社的运营成本为每人![]() 元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
(Ⅲ)若按照分层抽样的方法从年龄在![]() ,
, ![]() 的居民中抽取
的居民中抽取![]() 人进行旅游知识推广,并在知识推广后再抽取
人进行旅游知识推广,并在知识推广后再抽取![]() 人进行反馈,求进行反馈的居民中至少有
人进行反馈,求进行反馈的居民中至少有![]() 人的年龄在
人的年龄在![]() 的概率.
的概率.