Question

【题目】已知平面内一动点（）到点的距离与点到轴的距离的差等于1，

（1）求动点的轨迹的方程；

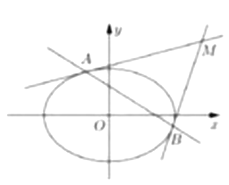
（2）过点的直线与轨迹相交于不同于坐标原点的两点，求面积的最小值．

Answer 1

【答案】（1）；（2）

【解析】

试题（1）根据平面内一动点到点的距离与点到y轴的距离的差等于1，可得当时，点到的距离等于点到直线的距离，所以动点的轨迹为抛物线；

（2）过点的直线的方程为，代入，可得，利用韦达定理，结合面积，即可求面积的最小值．

试题解析：（1）∵平面内一动点到点的距离与点到轴的距离的差等于1，

∴当时，点到的距离等于点到直线的距离，

∴动点的轨迹为抛物线，方程为（）；

∴动点的轨迹C的方程为（）；

（2）设点坐标为，点坐标为，

过点的直线的方程为，代入，可得，

，∴面积，

∴时，面积的最小值为2．