题目内容
已知函数![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)若数列![]()
![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若数列![]() 满足
满足![]() ,
,![]() 是数列
是数列![]() 前
前![]() 项的和,是否存在正实数
项的和,是否存在正实数![]() ,使不等式
,使不等式![]() 对于一切的
对于一切的![]() 恒成立?若存在指出
恒成立?若存在指出![]() 的取值范围,并证明;若不存在说明理由.
的取值范围,并证明;若不存在说明理由.
解:(1)令![]() ,
,![]() ,
,![]() ……2分
……2分
令![]() ,
,![]() ……5分
……5分
(2)∵![]() ①
①
∴![]() ②
②
由(Ⅰ),知 ![]()
∴①+②,得![]() …… 10分
…… 10分
(3)∵ ![]() ,∴
,∴ ![]()
∴![]() , ①
, ①
![]() , ②
, ②
①-②得![]()
即![]() …… 12分
…… 12分
要使得不等式![]() 恒成立,即
恒成立,即![]() 对于一切的
对于一切的![]() 恒成立,
恒成立,
![]()
设![]()
当![]() 时,由于对称轴直线
时,由于对称轴直线![]() ,且
,且 ![]() ,而函数
,而函数![]() 在
在![]() 是增函数,∴不等式
是增函数,∴不等式![]() 恒成立
恒成立
即当实数![]() 大于
大于![]() 时,不等式
时,不等式![]() 对于一切的
对于一切的![]() 恒成立 ……16分
恒成立 ……16分

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
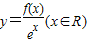 满足f′(x)>f(x),则f(1)与ef(0)的大小关系为( )
满足f′(x)>f(x),则f(1)与ef(0)的大小关系为( )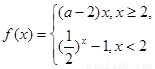 满足对任意的实数
满足对任意的实数 都有
都有 成立,则实数
成立,则实数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
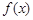 满足:①定义域为R;②
满足:①定义域为R;②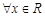 ,有
,有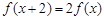 ;③当
;③当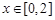 时,
时,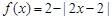 .记
.记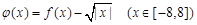 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数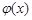 的零点个数为
( )
的零点个数为
( ) 满足
满足 ,且对于任意
,且对于任意 , 恒有
, 恒有 成立.
成立. 的值;
的值;  .
.