题目内容
已知椭圆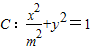 的左、右焦点分别为F1、F2,离心率为
的左、右焦点分别为F1、F2,离心率为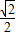 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=x+t(t>0)与椭圆C交于A,B两点.若原点O在以线段AB为直径的圆内,求实数t的取值范围.
【答案】分析:(Ⅰ)依题意,可知m>1,且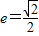 ,由此可m2=2,从而可得椭圆C的方程;
,由此可m2=2,从而可得椭圆C的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),则原点O在以线段AB为直径的圆内,等价于x1x2+y1y2<0,将直线与椭圆方程联立,利用韦达定理,可建立不等式,从而可求实数t的取值范围.
解答:解:(Ⅰ)依题意,可知m>1,且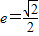 ,所以
,所以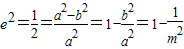 ,所以m2=2,即椭圆C的方程为
,所以m2=2,即椭圆C的方程为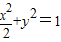 .…(5分)
.…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),则原点O在以线段AB为直径的圆内,等价于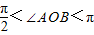 (A,O,B三点不共线),也就等价于
(A,O,B三点不共线),也就等价于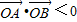 ,即x1x2+y1y2<0…①…(7分)
,即x1x2+y1y2<0…①…(7分)
联立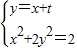 ,得3x2+4tx+2(t2-1)=0,所以△=16t2-24(t2-1)>0,即0<t2<3…②
,得3x2+4tx+2(t2-1)=0,所以△=16t2-24(t2-1)>0,即0<t2<3…②
且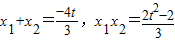 …(10分)
…(10分)
于是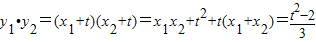
代入①式得,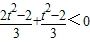 ,即
,即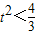 适合②式…(12分)
适合②式…(12分)
又t>0,所以解得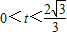 即求.…(13分)
即求.…(13分)
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查韦达定理,解题的关键是联立方程,运用韦达定理解题.
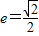 ,由此可m2=2,从而可得椭圆C的方程;
,由此可m2=2,从而可得椭圆C的方程;(Ⅱ)设A(x1,y1),B(x2,y2),则原点O在以线段AB为直径的圆内,等价于x1x2+y1y2<0,将直线与椭圆方程联立,利用韦达定理,可建立不等式,从而可求实数t的取值范围.
解答:解:(Ⅰ)依题意,可知m>1,且
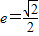 ,所以
,所以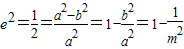 ,所以m2=2,即椭圆C的方程为
,所以m2=2,即椭圆C的方程为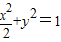 .…(5分)
.…(5分)(Ⅱ)设A(x1,y1),B(x2,y2),则原点O在以线段AB为直径的圆内,等价于
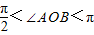 (A,O,B三点不共线),也就等价于
(A,O,B三点不共线),也就等价于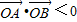 ,即x1x2+y1y2<0…①…(7分)
,即x1x2+y1y2<0…①…(7分)联立
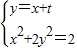 ,得3x2+4tx+2(t2-1)=0,所以△=16t2-24(t2-1)>0,即0<t2<3…②
,得3x2+4tx+2(t2-1)=0,所以△=16t2-24(t2-1)>0,即0<t2<3…②且
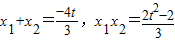 …(10分)
…(10分)于是
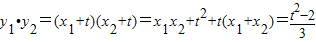
代入①式得,
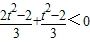 ,即
,即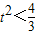 适合②式…(12分)
适合②式…(12分)又t>0,所以解得
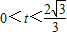 即求.…(13分)
即求.…(13分)点评:本题考查椭圆的标准方程,考查向量知识的运用,考查韦达定理,解题的关键是联立方程,运用韦达定理解题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线