题目内容
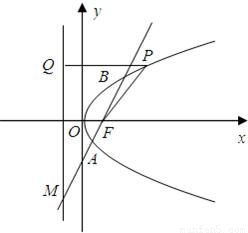
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且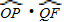 =
=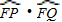 .
.(1)求动点P的轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M,已知
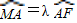 ,
,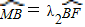 ,求λ1+λ2的值.
,求λ1+λ2的值.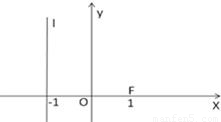
【答案】分析:解法一:(1)我们可设出点P的坐标(x,y),由直线l:x=-1,过P作直线l的垂线,垂足为点Q,则Q(-1,y),则我们根据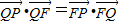 ,构造出一个关于x,y的方程,化简后,即可得到所求曲线的方程;
,构造出一个关于x,y的方程,化简后,即可得到所求曲线的方程;
(2)由过点F的直线交轨迹C于A、B两点,交直线l于点M,我们可以设出直线的点斜式方程,联立直线方程后,利用设而不求的思想,结合一元二次方程根与系数关系,易求λ1+λ2的值.
解法二:(1)由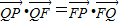 得
得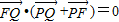 ,进而可得
,进而可得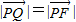 .根据抛物线的定义,我们易得动点的轨迹为抛物线,再由直线l(即准线)方程为:x=-1,易得抛物线方程;
.根据抛物线的定义,我们易得动点的轨迹为抛物线,再由直线l(即准线)方程为:x=-1,易得抛物线方程;
(2)由已知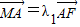 ,
,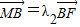 ,得λ1•λ2<0.根据抛物线的定义,可们可以将由已知
,得λ1•λ2<0.根据抛物线的定义,可们可以将由已知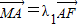 ,
,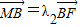 ,转化为
,转化为 ,进而求出λ1+λ2的值.
,进而求出λ1+λ2的值.
解答:解:法一:(Ⅰ)设点P(x,y),则Q(-1,y),
由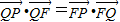 得:
得:
(x+1,0)•(2,-y)=(x-1,y)•(-2,y),
化简得C:y2=4x.
(Ⅱ)设直线AB的方程为:x=my+1(m≠0).
设A(x1,y1),B(x2,y2),又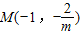 ,
,
联立方程组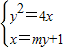 ,
,
消去x得:y2-4my-4=0,
∴△=(-4m)2+16>0,
故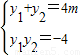
由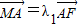 ,
,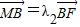 得:
得:
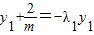 ,
,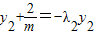 ,
,
整理得: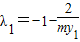 ,
,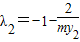 ,
,
∴ =
=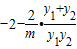 =
=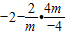 =0.
=0.
法二:(Ⅰ)由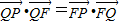 得:
得:
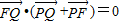 ,
,
∴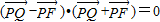 ,
,
∴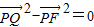 ,∴
,∴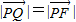 .
.
所以点P的轨迹C是抛物线,
由题意,轨迹C的方程为:y2=4x.
(Ⅱ)由已知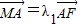 ,
,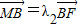 ,
,
得λ1•λ2<0.则:
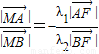 .①
.①
过点A,B分别作准线l的垂线,垂足分别为A1,B1,则有:
 .②
.②
由①②得: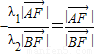 ,
,
即λ1+λ2=0.
点评:本小题主要考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.
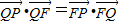 ,构造出一个关于x,y的方程,化简后,即可得到所求曲线的方程;
,构造出一个关于x,y的方程,化简后,即可得到所求曲线的方程;(2)由过点F的直线交轨迹C于A、B两点,交直线l于点M,我们可以设出直线的点斜式方程,联立直线方程后,利用设而不求的思想,结合一元二次方程根与系数关系,易求λ1+λ2的值.
解法二:(1)由
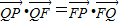 得
得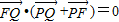 ,进而可得
,进而可得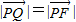 .根据抛物线的定义,我们易得动点的轨迹为抛物线,再由直线l(即准线)方程为:x=-1,易得抛物线方程;
.根据抛物线的定义,我们易得动点的轨迹为抛物线,再由直线l(即准线)方程为:x=-1,易得抛物线方程;(2)由已知
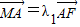 ,
,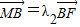 ,得λ1•λ2<0.根据抛物线的定义,可们可以将由已知
,得λ1•λ2<0.根据抛物线的定义,可们可以将由已知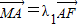 ,
,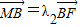 ,转化为
,转化为 ,进而求出λ1+λ2的值.
,进而求出λ1+λ2的值.解答:解:法一:(Ⅰ)设点P(x,y),则Q(-1,y),
由
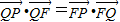 得:
得:(x+1,0)•(2,-y)=(x-1,y)•(-2,y),
化简得C:y2=4x.

(Ⅱ)设直线AB的方程为:x=my+1(m≠0).
设A(x1,y1),B(x2,y2),又
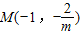 ,
,联立方程组
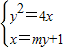 ,
,消去x得:y2-4my-4=0,
∴△=(-4m)2+16>0,
故
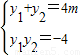
由
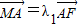 ,
,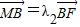 得:
得: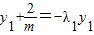 ,
,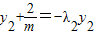 ,
,整理得:
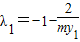 ,
,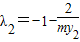 ,
,∴
 =
=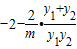 =
=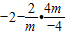 =0.
=0.法二:(Ⅰ)由
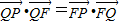 得:
得: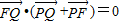 ,
,∴
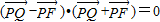 ,
,∴
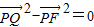 ,∴
,∴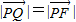 .
.所以点P的轨迹C是抛物线,
由题意,轨迹C的方程为:y2=4x.
(Ⅱ)由已知
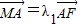 ,
,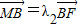 ,
,得λ1•λ2<0.则:
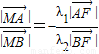 .①
.①过点A,B分别作准线l的垂线,垂足分别为A1,B1,则有:
 .②
.②由①②得:
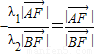 ,
,即λ1+λ2=0.
点评:本小题主要考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.

练习册系列答案
相关题目
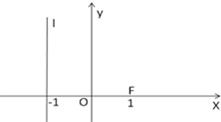 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且
 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若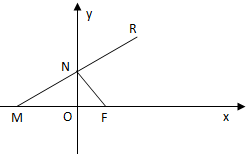 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且