题目内容
设动点
 到定点
到定点 的距离比到
的距离比到 轴的距离大
轴的距离大 .记点
.记点 的轨迹为曲线C.
的轨迹为曲线C.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ)设圆M过 ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上, 是圆M
在
是圆M
在 轴的截得的弦,当M
运动时弦长
轴的截得的弦,当M
运动时弦长 是否为定值?说明理由;
是否为定值?说明理由;
(Ⅲ)过 作互相垂直的两直线交曲线C于G、H、R、S,求四边形面
作互相垂直的两直线交曲线C于G、H、R、S,求四边形面 的最小值.
的最小值.
【答案】
解:(1) 由题意知,所求动点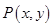 为以
为以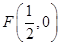 为焦点,直线
为焦点,直线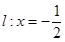 为准线的抛物线,方程为
为准线的抛物线,方程为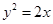 ;
;
(2) 设圆心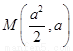 ,半径
,半径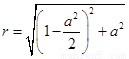
圆的方程为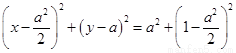
令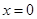 得
得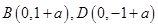
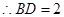
即弦长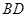 为定值;
为定值;
(3)设过F的直线方程为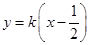 ,
,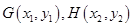
由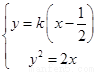 得
得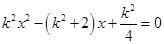
由韦达定理得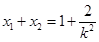
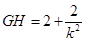
同理得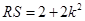
四边形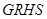 的面积
的面积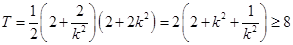 .
.
【解析】略

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
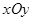 中,设动点
中,设动点 到定点
到定点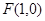 的距离与到定直线
的距离与到定直线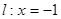 的距离相等,记
的距离相等,记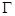 .又直线
.又直线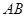 的一个方向向量
的一个方向向量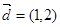 且过点
且过点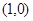 ,
,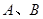 两点,求
两点,求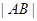 的长.
的长.
 到定点
到定点 的距离比到
的距离比到 轴的距离大
轴的距离大 .记点
.记点 的轨迹为曲线C.
的轨迹为曲线C. ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上, 是圆M 在
是圆M 在 的最小值.
的最小值.