题目内容
设f(x)是定义在R上的增函数,若不等式f(1-ax-
解析:∵f(x)是R上的增函数. ∴不等式f(1-ax-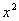 )<f(2-a) 对任意x∈[0,1]都成立.
)<f(2-a) 对任意x∈[0,1]都成立.
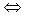 不等式1-ax-
不等式1-ax-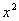 <2-a 对任意x∈[0,1]都成立
<2-a 对任意x∈[0,1]都成立 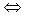
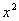 +ax-a+1>0 对任意x∈[0,1]都成立①
+ax-a+1>0 对任意x∈[0,1]都成立①
解法一: (向最值问题转化,以对称轴的位置为主线展开讨论.)
令g(x)=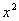 +ax-a+1,
+ax-a+1,
则①式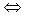 g(x)>0对任意x∈[0,1]都成立.
g(x)>0对任意x∈[0,1]都成立.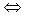 g(x)在区间[0,1]上的最小值大于0.②注意到g(x)图象的对称轴为x=-
g(x)在区间[0,1]上的最小值大于0.②注意到g(x)图象的对称轴为x=-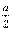
(1)当-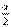 ≤0即a≥0时, 由②得g(0)>0
≤0即a≥0时, 由②得g(0)>0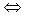 -a+1>0
-a+1>0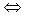 a<1,即0≤a<1;
a<1,即0≤a<1;
(2)当0<-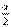 ≤1时,即-2≤a<0时, 由②得g(-
≤1时,即-2≤a<0时, 由②得g(-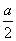 )>0
)>0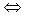 1-a-
1-a-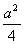 >0
>0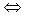
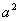 +4a-4<0
+4a-4<0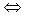
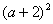 <8
<8
当-2≤a<0时,这一不等式也能成立.
(3)当-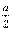 >1即a<-2时.由②得g(1)>0
>1即a<-2时.由②得g(1)>0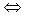 2>0即当a<-2时,不等式成立.
2>0即当a<-2时,不等式成立.
于是综合(1)(2)(3)得所求实数a的取值范围为[0,1)∪[-2,0]∪(-∞,-2), 即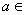 (-∞,1).
(-∞,1).
解法二: (以△的取值为主线展开讨论)对于二次三项式g(x)=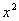 +ax-a+1,
+ax-a+1,
其判别式△=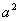 +4(a-1) =
+4(a-1) =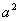 +4a-4△<0
+4a-4△<0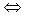
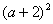 <8
<8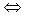
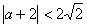
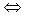 -
-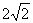 -2<a<
-2<a<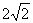 -2
-2
(1)当△<0时,g(x)>0对任意x∈[0,1]都成立,此时-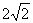 -2<a<
-2<a<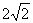 -2;
-2;
(2)当△≥0时,由g(x)>0对任意x∈[0,1]都成立得
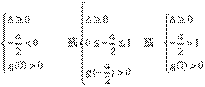
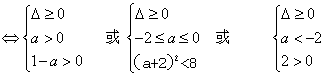
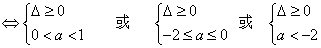
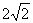 -2≤a<1 或a≤-
-2≤a<1 或a≤-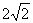 -2.
-2.
于是由(1)(2)得所求a的取值范围为(-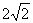 -2,
-2,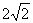 -2)∪[
-2)∪[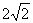 -2,1)∪(-∞, -
-2,1)∪(-∞, -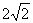 -2] 即
-2] 即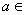 (-∞,1).
(-∞,1).
解法一: (向最值问题转化,以对称轴的位置为主线展开讨论.)
令g(x)=
则①式
(1)当-
(2)当0<-
当-2≤a<0时,这一不等式也能成立.
(3)当-
于是综合(1)(2)(3)得所求实数a的取值范围为[0,1)∪[-2,0]∪(-∞,-2), 即
解法二: (以△的取值为主线展开讨论)对于二次三项式g(x)=
其判别式△=
(1)当△<0时,g(x)>0对任意x∈[0,1]都成立,此时-
(2)当△≥0时,由g(x)>0对任意x∈[0,1]都成立得

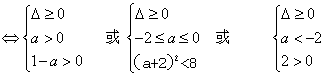
于是由(1)(2)得所求a的取值范围为(-

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目



 )x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是 ) D. (
) D. (