Question

16．在三棱锥P-ABC中，△PAB是等边三角形，PA⊥AC，PB⊥BC．
（1）证明：AB⊥PC；
（2）若PC=2，且平面PAC⊥平面PBC，求三棱锥P-ABC的体积．

Answer 1

分析 （1）求出AC和BC，取AB中点M，连结PM，CM，说明AB⊥PM，AB⊥MC，证明AB⊥平面PMC，然后证明AB⊥PC．
（2）在平面PAC内作AD⊥PC，垂足为D，连结BD，证明ABD为等腰直角三角形，设AB=PA=PB=a，求解a，然后求解底面面积以及体积即可．

解答 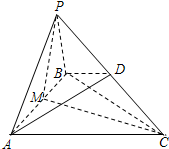解：（1）证明：在Rt△PAC和Rt△PBC中$AC=\sqrt{P{C^2}-P{A^2}}，BC=\sqrt{P{C^2}-P{B^2}}$$2\sqrt{7}$
取AB中点M，连结PM，CM，则AB⊥PM，AB⊥MC，
∴AB⊥平面PMC，而PC?平面PMC，∴AB⊥PC…（6分）
（2）在平面PAC内作AD⊥PC，垂足为D，连结BD
∵平面PAC⊥平面PBC，∴AD⊥平面PBC，又BD?平面PBC，
∴AD⊥BD，又Rt△PAC≌RtPBC，
∴AD=BD，∴△ABD为等腰直角三角形    …（9分）
设AB=PA=PB=a，则$AD=\frac{{\sqrt{2}}}{2}a$
在Rt△PAC中：由PA•AC=PC•AD，
得$a•\sqrt{4-{a^2}}=2×\frac{{\sqrt{2}}}{2}a$，
解得$a=\sqrt{2}$…（11分）
∴${S_{△ABD}}=\frac{1}{2}AD•BD=\frac{1}{2}{（\frac{{\sqrt{2}}}{2}a）^2}=\frac{1}{2}$，
∴${V_{P-ABC}}=\frac{1}{3}{S_{△ABD}}•PC=\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}$．…（13分）

点评 本题考查几何体的体积的求法，直线与平面垂直的判定与性质的应用，考查空间想象能力以及计算能力．