题目内容
(本小题满分12分)已知函数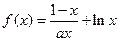 .
.
(Ⅰ)若函数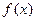 在
在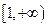 上是增函数,求正实数
上是增函数,求正实数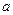 的取值范围;
的取值范围;
(Ⅱ)若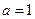 ,
,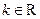 且
且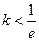 ,设
,设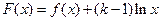 ,求函数
,求函数 在
在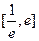 上的最大值和最小值.
上的最大值和最小值.
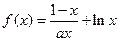 .
.(Ⅰ)若函数
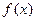 在
在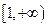 上是增函数,求正实数
上是增函数,求正实数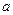 的取值范围;
的取值范围;(Ⅱ)若
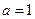 ,
,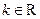 且
且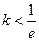 ,设
,设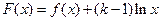 ,求函数
,求函数 在
在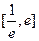 上的最大值和最小值.
上的最大值和最小值.(Ⅰ)解:由题设可得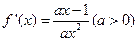
因为函数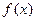 在
在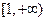 上是增函数,
上是增函数,
所以,当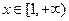 时
时 ,不等式
,不等式 即
即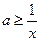 恒成立
恒成立
因为,当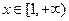 时,
时, 的最大值为
的最大值为 ,则实数
,则实数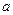 的取值范围是
的取值范围是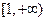 -----4分
-----4分
(Ⅱ) 解: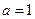 ,
,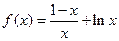

所以,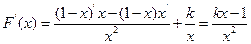 …………6分
…………6分
(1) 若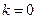 ,则
,则 ,在
,在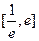 上, 恒有
上, 恒有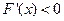 ,
,
所以 在
在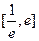 上单调递减
上单调递减
 ,
,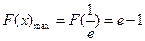 …………7分
…………7分
(2)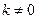 时
时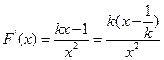
(i)若 ,在
,在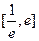 上,恒有
上,恒有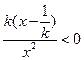
所以 在
在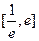 上单调递减
上单调递减

 …………9分
…………9分
ii)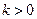 时,因为
时,因为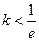 ,所以
,所以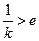
 ,所以
,所以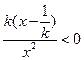
所以 在
在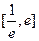 上单调递减
上单调递减
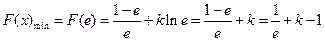
 …………11分
…………11分
综上所述:当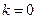 时,
时,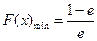 ,
, ;当
;当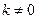
且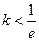 时,
时,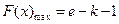 ,
,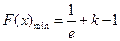 .…………12分
.…………12分
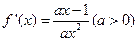
因为函数
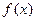 在
在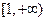 上是增函数,
上是增函数,所以,当
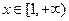 时
时 ,不等式
,不等式 即
即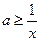 恒成立
恒成立因为,当
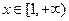 时,
时, 的最大值为
的最大值为 ,则实数
,则实数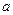 的取值范围是
的取值范围是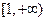 -----4分
-----4分(Ⅱ) 解:
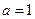 ,
,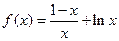

所以,
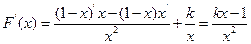 …………6分
…………6分(1) 若
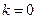 ,则
,则 ,在
,在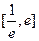 上, 恒有
上, 恒有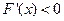 ,
,所以
 在
在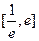 上单调递减
上单调递减 ,
,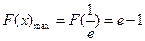 …………7分
…………7分(2)
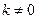 时
时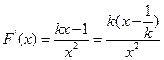
(i)若
 ,在
,在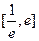 上,恒有
上,恒有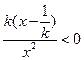
所以
 在
在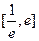 上单调递减
上单调递减
 …………9分
…………9分ii)
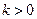 时,因为
时,因为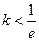 ,所以
,所以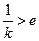
 ,所以
,所以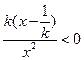
所以
 在
在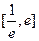 上单调递减
上单调递减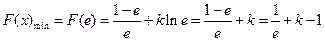
 …………11分
…………11分综上所述:当
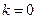 时,
时,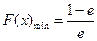 ,
, ;当
;当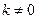
且
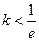 时,
时,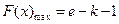 ,
,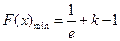 .…………12分
.…………12分略

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
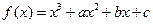 是定义在
是定义在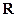 上的奇函数,其图象过点
上的奇函数,其图象过点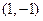 和
和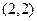 .
.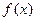 的解析式,并求
的解析式,并求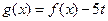 ,当实数
,当实数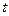 如何取值时,关于
如何取值时,关于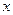 的方程
的方程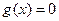 有且只有一个实
有且只有一个实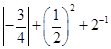 的结果相同的是( ).
的结果相同的是( ).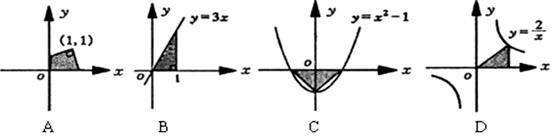
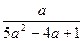 对称,求b的最小值.
对称,求b的最小值.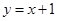 上的一点向圆
上的一点向圆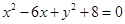 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )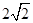
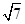
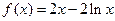
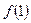 )的切线方程
)的切线方程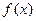 的极值
的极值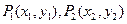 ,如果存在曲线上的点
,如果存在曲线上的点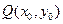 ,且
,且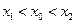 ,使得曲线在点
,使得曲线在点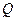 处的切线
处的切线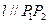 ,则称
,则称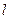 为弦
为弦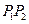 的陪伴切线.已知两点
的陪伴切线.已知两点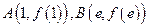 ,试求弦
,试求弦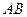 的陪伴切线
的陪伴切线 的导数
的导数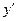 =__________________.
=__________________.
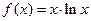 的单调递减区间是 .
的单调递减区间是 .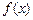 的定义域为
的定义域为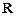 ,
,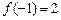 ,对任意
,对任意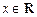 ,
,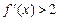 ,则
,则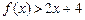 的解集为( )
的解集为( )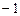 ,+
,+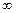 )
)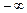 ,
,