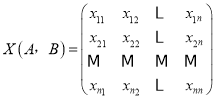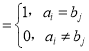题目内容
【题目】已知![]() 是定义域为
是定义域为![]() 的偶函数,对
的偶函数,对![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() ,函数
,函数![]() .现给出以下命题:①
.现给出以下命题:①![]() 是周期函数;②
是周期函数;②![]() 的图象关于直线
的图象关于直线![]() 对称;③当
对称;③当![]() 时,
时,![]() 在
在![]() 内有一个零点;④当
内有一个零点;④当![]() 时,
时,![]() 在
在![]() 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.
【答案】①②④
【解析】
①根据![]() ,有
,有![]() ,利用周期函数的定义判断;②根据
,利用周期函数的定义判断;②根据![]() 是定义域为
是定义域为![]() 的偶函数,有
的偶函数,有![]() ,再结合
,再结合![]() 判断;③令
判断;③令![]() ,即
,即![]() ,在同一坐标系中作出
,在同一坐标系中作出![]() ,用数形结合法判断;④在同一坐标系中作出
,用数形结合法判断;④在同一坐标系中作出![]() ,用数形结合法判断.
,用数形结合法判断.
①因为对![]() ,有
,有![]() ,所以
,所以![]() 是周期函数,故正确;
是周期函数,故正确;
②因为![]() 是定义域为
是定义域为![]() 的偶函数,所以
的偶函数,所以![]() ,又因为对
,又因为对![]() ,有
,有![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() 的图象关于直线
的图象关于直线![]() 对称,故正确;
对称,故正确;
③当![]() 时,令
时,令![]() ,
,
即![]() ,在同一坐标系中作出
,在同一坐标系中作出![]()
![]() 的图象如图所示:
的图象如图所示:
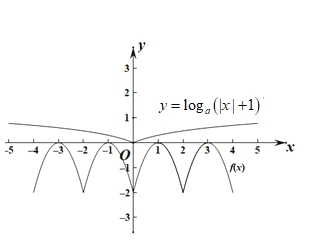
所以![]() 在
在![]() 内无零点,故错误;
内无零点,故错误;
④当![]() 时,令
时,令![]() ,
,
在同一坐标系中作出![]() ,
,![]()
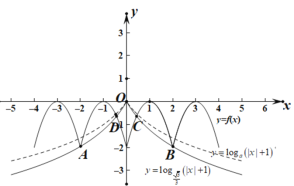
的图象如下图所示:
![]() ,
,
而![]() ,
,
当![]() 时,
时,![]() 与
与![]() 至少有三个交点,
至少有三个交点,
![]() 与
与![]() 为偶函数,
为偶函数,
![]() 与
与![]() 至少有六个交点,
至少有六个交点,
所以![]() 在
在![]() 上至少有六个零点,故正确.
上至少有六个零点,故正确.
所以正确命题的序号为①②④
故答案为:①②④

练习册系列答案
相关题目