题目内容
若函数f（x）=-cos2x+
（x∈R），则f（x）是
- A.最小正周期为
的奇函数 - B.最小正周期为π的奇函数
- C.最小正周期为
的偶函数 - D.最小正周期为π的偶函数
D
分析：把函数解析式第一项利用二倍角的余弦函数公式化简，合并整理为一个角的余弦函数，根据余弦函数为偶函数，同时找出ω的值，代入周期公式T=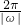
求出函数的最小正周期，即可得到正确的选项．
解答：函数f（x）=-cos2x+=-
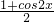+=-cos2x，
∵ω=2，∴T=
=π，
又cos2x为偶函数，
则函数为最小正周期为π的偶函数．
故选D
点评：此题考查了三角函数的周期性及其求法，涉及的知识有：二倍角的余弦函数公式，周期公式，以及余弦函数的奇偶性，其中利用三角函数的恒等变形把函数解析式化为一个角的余弦函数是解本题的关键．
分析：把函数解析式第一项利用二倍角的余弦函数公式化简，合并整理为一个角的余弦函数，根据余弦函数为偶函数，同时找出ω的值，代入周期公式T=
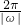求出函数的最小正周期，即可得到正确的选项．解答：函数f（x）=-cos2x+
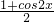=-+=-cos2x，∵ω=2，∴T=
=π，又cos2x为偶函数，
则函数为最小正周期为π的偶函数．
故选D
点评：此题考查了三角函数的周期性及其求法，涉及的知识有：二倍角的余弦函数公式，周期公式，以及余弦函数的奇偶性，其中利用三角函数的恒等变形把函数解析式化为一个角的余弦函数是解本题的关键．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
若函数f（x）对定义域R内的任意x都有f（x）=f（2-x），且当x≠1时其导函数f′（x） 满足xf′（x）＞f′（x），若1＜a＜2，则（ ）
| A、f（2a）＜f（2）＜f（log2a） | B、f（log2a）＜f（2）＜f（2a） | C、f（2）＜f（log2a）＜f（2a） | D、f（log2a）＜f（2a）＜f（2） |