题目内容
设函数f(x)为R上的增函数,令g(x)=f(x)-f(2-x).(1)求证:g(x)为R上的增函数;
(2)若g(x1)+g(x2)>0,求证:x1+x2>2.
证明:(1)任取x1<x2∈R,则有2-x1>2-x2.
∵f(x)为R上的增函数,
∴f(x1)<f(x2),f(2-x1)>f(2-x2).
∴g(x2)-g(x1)=[f(x2)-f(2-x2)]-[f(x1-f(2-x1))]=[f(x2)-f(x1)]+[f(2-x1)-f(2-x2)]>0.
∴g(x2)>g(x1),g(x)为R上的增函数.
(2)∵g(x1)+g(x2)>0,
∴g(x1)>-g(x2),
∴g(x1)>f(2-x2)-f(x2).
又g(2-x2)=f(2-x2)-f(x2),
∴g(x1)>g(2-x2),∴x1>2-x2,
∴x1+x2>2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

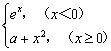 为R上的连续函数,则a等于( )
为R上的连续函数,则a等于( )