题目内容
已知椭圆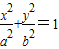 的一条弦所在直线方程是x-y+3=0,弦的中点坐标是(-2,1),则椭圆的离心率是( )
的一条弦所在直线方程是x-y+3=0,弦的中点坐标是(-2,1),则椭圆的离心率是( )A.

B.
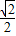
C.
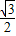
D.
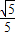
【答案】分析:设出以M为中点的弦的两个端点的坐标,代入椭圆的方程相减,把中点公式代入,可得弦的斜率与a,b的关系式,从而求得椭圆的离心率.
解答:解:显然M(-2,1)在椭圆内,设直线与椭圆的交点A(x1,y1),B(x2,y2),
则 +
+ =1,
=1, +
+ =1,相减得:
=1,相减得: =0,
=0,
整理得:k=- =1,
=1,
又弦的中点坐标是(-2,1),
∴ ,
,
∴ ,
,
则椭圆的离心率是e= =
= =
= .
.
故选B.
点评:本题考查椭圆的标准方程和简单性质,中点公式及斜率公式的应用,以及直线方程,属于基础题.本题解题中直接利用点差法巧妙用上了中点坐标公式与弦的斜率,方法极为巧妙,此方法即为通常所说的点差法,研究弦中点问题时经常采用此方法
解答:解:显然M(-2,1)在椭圆内,设直线与椭圆的交点A(x1,y1),B(x2,y2),
则
 +
+ =1,
=1, +
+ =1,相减得:
=1,相减得: =0,
=0,整理得:k=-
 =1,
=1,又弦的中点坐标是(-2,1),
∴
 ,
,∴
 ,
,则椭圆的离心率是e=
 =
= =
= .
.故选B.
点评:本题考查椭圆的标准方程和简单性质,中点公式及斜率公式的应用,以及直线方程,属于基础题.本题解题中直接利用点差法巧妙用上了中点坐标公式与弦的斜率,方法极为巧妙,此方法即为通常所说的点差法,研究弦中点问题时经常采用此方法

练习册系列答案
相关题目
 的一条弦所在直线方程是x-y+3=0,弦的中点坐标是(-2,1),则椭圆的离心率是
的一条弦所在直线方程是x-y+3=0,弦的中点坐标是(-2,1),则椭圆的离心率是



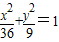 的一条弦被点A(4,2)平分,那么这条弦所在的直线的斜率为
的一条弦被点A(4,2)平分,那么这条弦所在的直线的斜率为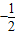 ;
;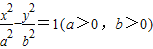 的焦点到渐近线的距离为b.
的焦点到渐近线的距离为b.