题目内容

定义在实数R上的函数y= f（x）是偶函数，当x≥0时，.

（Ⅰ）求f（x）在R上的表达式；

（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）.

解析：（Ⅰ）设x＜0，则- x＞0，   ∵f（x）是偶函数，

∴f（-x）=f（x） ∴x＜0时，  所以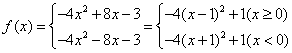  

（Ⅱ）y=f（x）开口向下，所以y=f（x）有最大值f（1）=f（-1）=1

     函数y=f（x）的单调递增区间是（-∞，-1和[0，1]   

单调递减区间是 [-1，0]和[1，+∞ 
练习册系列答案
相关题目
定义在实数R上的函数y=f（x）是偶函数，当x≥0时，f（x）=-4x2+8x-3．
（Ⅰ）求f（x）在R上的表达式；
（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）．
函数f（x）是幂函数，图象过（2，8），定义在实数R上的函数y=F（x）是奇函数，当x＞0时，F（x）=f（x）+1，求F（x）在R上的表达式；并画出图象．
已知定义在实数R上的函数y=f（x）不恒为零，同时满足f（x+y）=f（x）f（y），且当x＞0时，f（x）＞1，那么当x＜0时，一定有（　　）
A、f（x）＜-1B、-1＜f（x）＜0C、f（x）＞1D、0＜f（x）＜1
设f（x）是定义在实数R上的函数，g（x）是定义在正整数N*上的函数，同时满足下列条件：
（1）任意x，y∈R，有f（x+y）=f（x）f（y），当x＜0时，f（x）＞1且f(-1)=
5
；
（2）g（1）=f（0），g（2）=f（-2）；
（3）f[g(n+2)]=
f[(n+3)g(n+1)]
f[(n+2)g(n)]
，n∈N*
试求：
（1）证明：任意x，y∈R，x≠y，都有
f(x)-f(y)
x-y
＜0；
（2）是否存在正整数n，使得g（n）是25的倍数，若存在，求出所有自然数n；若不存在说明理由．（阶乘定义：n!=1×2×3×…×n）
函数f（x）是幂函数，图象过点（2，8），定义在实数R上的函数y=F（x）是奇函数，当x＞0时，F（x）=f（x）+1，求F（x）在R上的表达式；并画出图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网