Question

（本题满分12分）

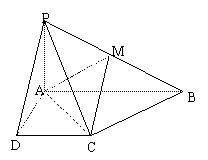已知四棱锥的底面是直角梯形，底面ABCD，是PB的中点.

（I）证明：平面平面PCD；

（II）求AC与PB所成的角；

（III）求平面AMC与平面BMC所成角的大小.

Answer 1

方法一：（I）证明：底面，

由三垂线定理得，则平面PAD，

平面平面PAD.

（II）解：过点B作，且，则是AC与PB所成的角.

            与底面ABCD所成的角.

                则

                又

              是等腰直角三角形，

            则

            与PB所成的角为

（III）解：作，垂足为N，连接BN.在直角中，又

              得

              则是所求二面角的平面角.

              ，得面PAC，

              在直角中，，所以

              在等腰中用等积变换，

             

             

             

              则所求的二面角为

方法二：底面ABCD，构成空间坐标系，各点坐标是

（I）证明：，由得

        由得则平面PAD.

        所以平面平PAD.

（II）解：

       所以AC与PB所成的角为

（III）解：在MC上取一点，则，

        ，要使，则需

        即，解得由得，则N点坐标为       从而为     所求二面角的平面角。

        所以所求二面角为