题目内容
3.设集合A={x|-1≤x≤2},B={x|x2-(2m+1)x+2m<0}.(1)当m<$\frac{1}{2}$时,把集合B用区间表达;
(2)若A∪B=A,求实数m的取值范围.
分析 x2-(2m+1)x+2m<0?(x-1)(x-2m)<0,
(1)由m<$\frac{1}{2}$知,2m<1,从而确定集合B;
(2)由A∪B=A,可知B⊆A,又A={x|-1≤x≤2},讨论集合B即可
解答 解:∵不等式x2-(2m+1)x+2m<0?(x-1)(x-2m)<0.
(1)当m<$\frac{1}{2}$时,2m<1,∴集合B={x|2m<x<1}=(2m,1)
(2)若A∪B=A,则B⊆A,∵A={x|-1≤x≤2},
①当m<$\frac{1}{2}$时,B={x|2m<x<1},此时-1≤2m<1⇒-$\frac{1}{2}$≤m<$\frac{1}{2}$;
②当m=$\frac{1}{2}$时,B=?,有B⊆A成立;
③当m>$\frac{1}{2}$时,B={x|1<x<2m},此时1<2m≤2⇒$\frac{1}{2}$<m≤1;
综上所述,所求m的取值范围是-$\frac{1}{2}$≤m≤1.
点评 本题考查了集合的化简与集合的运算的应用,同时考查了集合的包含关系与集合运算的转化,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
11.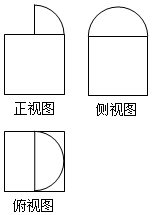 一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )
一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )
 一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )
一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )| A. | $8+\frac{π}{3}$ | B. | $8+\frac{π}{4}$ | C. | $8+\frac{4π}{3}$ | D. | $4+\frac{π}{3}$ |
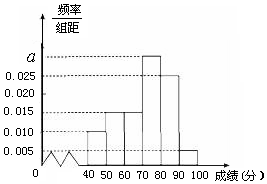 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: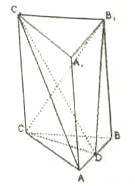 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.