题目内容
已知圆C的半径为2,圆心在 轴正半轴上,直线
轴正半轴上,直线 与圆C相切
与圆C相切
(1)求圆C的方程;
(2)过点 的直线
的直线 与圆C交于不同的两点
与圆C交于不同的两点 且为
且为 时
时
求: 的面积.
的面积.
(1)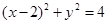 ;(2)
;(2)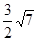 .
.
解析试题分析:(1)半径已知,所以只需确定圆心即可,设圆心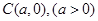 ,因为直线
,因为直线 与圆相切,利用圆心到直线的距离
与圆相切,利用圆心到直线的距离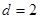 列式求
列式求 ;(2)从
;(2)从 可以看出,这是韦达定理的特征,故把直线方程设为
可以看出,这是韦达定理的特征,故把直线方程设为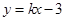 ,与(1)所求圆的方程联立,得关于
,与(1)所求圆的方程联立,得关于 的一元二次方程,用含有
的一元二次方程,用含有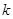 的代数式表示出
的代数式表示出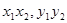 ,进而利用
,进而利用 列方程,求
列方程,求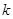 ,然后用弦长公式求
,然后用弦长公式求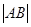 ,用点到直线的距离公式求高,面积可求.
,用点到直线的距离公式求高,面积可求.
试题解析:(I)设圆心为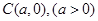 ,则圆C的方程为
,则圆C的方程为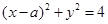
因为圆C与 相切 所以
相切 所以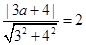 解得:
解得: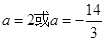 (舍)
(舍)
所以圆C的方程为: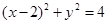 4分
4分
(II)依题意:设直线l的方程为: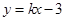
由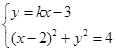 得
得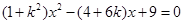
∵l与圆C相交于不同两点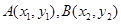
∴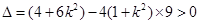
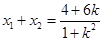
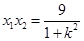
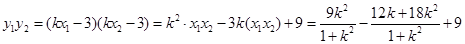
又∵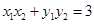 ∴
∴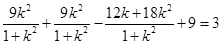
整理得: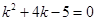 解得
解得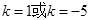 (舍)
(舍)
∴直线l的方程为: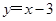 8分
8分
圆心C到l的距离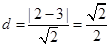 在△ABC中,|AB|=
在△ABC中,|AB|=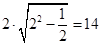
原点O到直线l的距离,即△AOB底边AB边上的高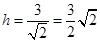
∴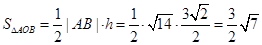 12分
12分
考点:1、直线和圆的位置关系;2、圆的方程;3、弦长公式和点到直线的距离公式和韦达定理.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 ,圆
,圆 的直径为
的直径为 的长轴.如图,
的长轴.如图, 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点 两点,
两点, 垂直于
垂直于 .
.
 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆 、
、 两点,且
两点,且 ,求圆
,求圆 ,直线
,直线  ,
,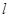 与圆
与圆 交与
交与 两点,点
两点,点 .
. 时,求
时,求 的值;
的值; 时,求
时,求 ,直线
,直线 .
. 与圆C的位置关系;
与圆C的位置关系; ,求此时直线
,求此时直线 及直线
及直线 . 当直线
. 当直线 被圆
被圆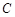 截得的弦长为
截得的弦长为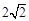 时, 求(1)
时, 求(1) 的值; (2)求过点
的值; (2)求过点 并与圆
并与圆 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
.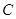 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆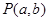 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,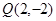 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 轴的交点为
轴的交点为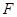 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 过点
过点 截直线
截直线 的弦长为
的弦长为 ;
; 的值;
的值;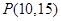 的圆的切线所在的直线方程.
的圆的切线所在的直线方程.