题目内容
已知函数![]() R)。
R)。
(1)当![]() 时,求
时,求![]() 在区间[1,
在区间[1,![]() ]上的最大值和最小值;
]上的最大值和最小值;
(2)如果函数![]() 、
、![]() 、
、![]() 在公共定义域D上满足
在公共定义域D上满足![]()
![]()
![]() ,那么就称
,那么就称![]() 为
为![]() 、
、![]() 的“活动函数” .已知函数
的“活动函数” .已知函数![]() ,
,![]() 。若在区间(1,
。若在区间(1,![]() )上,函数
)上,函数![]() 是
是![]() 、
、![]() 的“活动函数”,求
的“活动函数”,求![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,
时,![]() ,
,![]() ,对于
,对于![]() ,有
,有![]() ,∴
,∴![]() 在区间[1,
在区间[1,![]() ]上为增函数。
]上为增函数。
∴![]() ,
,![]() 。(4分)
。(4分)
(2)在区间(1,![]() )上,函数
)上,函数![]() 是
是![]() 、
、![]() 的“活动函数”,则
的“活动函数”,则![]()
![]()
![]() ,
,
令![]() ,对于
,对于![]() (1,
(1,![]() )恒成立。
)恒成立。
令![]() ,对于
,对于![]() (1,
(1,![]() )恒成立。
)恒成立。
∵![]() ,
,
![]() ,
,
∴![]() 在(1,
在(1,![]() )上递减,只要
)上递减,只要![]() ,即可得
,即可得![]() ,解得
,解得![]() 。
。
而![]() 对于
对于![]() (1,
(1,![]() )且
)且![]() 有
有![]() 。
。![]() 在(1,
在(1,![]() )递减。
)递减。
只要![]() 即可,
即可,![]() ,解得
,解得![]() ,
,
所以![]() 。 (12分)
。 (12分)

练习册系列答案
相关题目
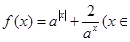 R,
R,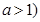 ,
,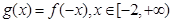 ,若
,若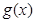 的最小值与
的最小值与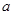 无关,求
无关,求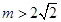 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于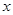 的方程
的方程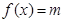 的解集
的解集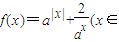 R,a>1),
R,a>1), ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.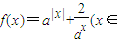 R,a>1),
R,a>1),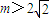 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.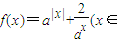 R,a>1),
R,a>1),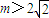 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.