题目内容
已知函数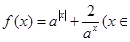 R,
R,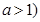 ,
,
(1)求函数f(x)的值域;
(2)记函数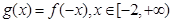 ,若
,若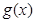 的最小值与
的最小值与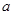 无关,求
无关,求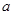 的取值范围;
的取值范围;
(3)若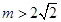 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于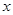 的方程
的方程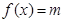 的解集
的解集
【答案】
(1) ;(2)
;(2) ;(3)①
;(3)① 时,解集为
时,解集为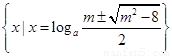 ;
;
②m>3时,解集为 或
或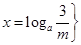
【解析】
试题分析:(1)因解析式中有绝对值,,则把 分情况利用基本不等式讨论函数
分情况利用基本不等式讨论函数 的值域;(2)易得函数
的值域;(2)易得函数 的解析式,再分情况去掉绝对值,利用基本不等求函数的最小值,从而得结论;(3)分
的解析式,再分情况去掉绝对值,利用基本不等求函数的最小值,从而得结论;(3)分 两种情况求方程的解
两种情况求方程的解
试题解析:(1)① 时,
时,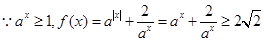 ,
,
当且仅当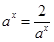 ,即
,即 时等号成立;
时等号成立;
② ,
, ,由①②知函数
,由①②知函数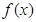 的值域为
的值域为
(2) ,
,
① ,
, ,
,
② 时,
时,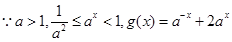 ,
,
令 ,则
,则 ,记
,记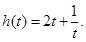
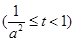 ,
,
 ,当且仅当
,当且仅当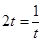 ,
, 时等号成立,
时等号成立,
(i) ,即
,即 时,结合①知
时,结合①知 与
与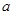 无关;
无关;
(ii)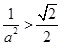 ,即
,即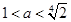 时,
时, ,
,
 在
在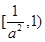 上是增函数,
上是增函数, ,
,
结合①知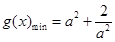 与
与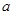 有关;
有关;
综上,若 的最小值与
的最小值与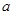 无关,则实数
无关,则实数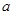 的取值范围是
的取值范围是
(3)① 时,关于
时,关于 的方程
的方程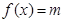 的解集为
的解集为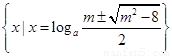 ;
;
②m>3时,关于x的方程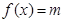 的解集为
的解集为 或
或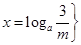
考点:1、利用不等式求函数的值域;2、利用不等式或导数求最值;3、解指数方程

练习册系列答案
相关题目
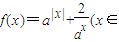 R,a>1),
R,a>1), ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.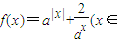 R,a>1),
R,a>1),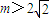 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.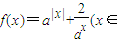 R,a>1),
R,a>1),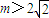 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.