题目内容
若直线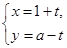 (
(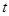 为参数)被圆
为参数)被圆 (
(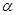 为参数)所截的弦长为
为参数)所截的弦长为 ,则
,则 的值为( )
的值为( )
A.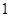 或 或 | B.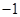 或 或 |
C.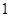 或 或 | D.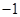 或 或 |
A
解析试题分析:直线为 ,圆为
,圆为 ,即
,即 ,半弦长为
,半弦长为 ,∴点
,∴点 到直线的距离为
到直线的距离为 ,即
,即 ,则
,则 或
或 .
.
考点:参数方程与普通方程的互化、点到直线的距离公式.

练习册系列答案
相关题目
若曲线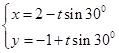 (
( 为参数) 与曲线
为参数) 与曲线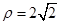 相交于
相交于 ,
, 两点,则
两点,则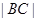 的值为( ).
的值为( ).
A.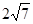 | B.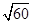 | C.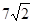 | D.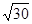 |
设r>0,那么直线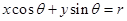 (
(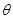 是常数)与圆
是常数)与圆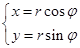 (
(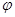 是参数)的位置关系是
是参数)的位置关系是
| A.相交 | B.相切 | C.相离 | D.视r的大小而定 |
极坐标方程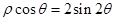 表示的曲线为
表示的曲线为
| A.一条射线和一个圆 | B.两条直线 |
| C.一条直线和一个圆 | D.一个圆 |
在平面直角坐标系中,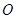 为原点,
为原点,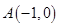 ,
,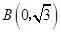 ,
,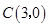 ,动点
,动点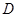 满足
满足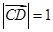 ,
,
则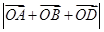 的取值范围是( )
的取值范围是( )
A.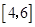 | B.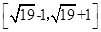 |
C.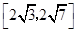 | D.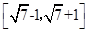 |
在极坐标系中,直线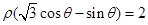 与圆
与圆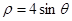 的交点的极坐标为( )
的交点的极坐标为( )
A.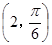 | B.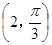 | C.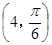 | D.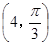 |
在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A.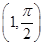 | B.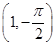 | C.(1,0) | D.(1,π) |
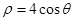 上的点到直线
上的点到直线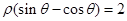 的最大距离为 .
的最大距离为 .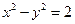
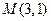 为中点的弦所在的直线的方程
为中点的弦所在的直线的方程 的弦的中点的轨迹方程
的弦的中点的轨迹方程