题目内容
已知数列{an}、{bn}满足a1=1,a2=3, ,bn=an+1-an.
,bn=an+1-an.
(1)求数列{bn}的通项公式;
(2)求数列{an}的通项公式;
(3)数列{cn}满足cn=log2(an+1)(n∈N*),求
解:(1)∵ ,又b1=a2-a1=3-1=2.
,又b1=a2-a1=3-1=2.
所以数列{bn}是首项b1=2,公比q=2的等比数列.故bn=b1qn-1=2n
(2)an+1-an=2n(n∈N*)
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1= .
.
(3)cn=log2(an+1)=log2(2n-1+1)=log22n=n,(n∈N*),
∴
∴ =
= =
=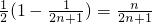
分析:(1)由题意可知数列{bn}是首项b1=2,公比q=2的等比数列.故bn=b1qn-1=2n.
(2)由an+1-an=2n(n∈N*)可知an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,由此能够求出数列{an}的通项公式.
(3)根据题意,可知 ,由此能够求出答案.
,由此能够求出答案.
点评:本题考查数列的性质和应用,具有一定的难度,解题时要注意公式的合理选用.
 ,又b1=a2-a1=3-1=2.
,又b1=a2-a1=3-1=2.所以数列{bn}是首项b1=2,公比q=2的等比数列.故bn=b1qn-1=2n
(2)an+1-an=2n(n∈N*)
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=
 .
.(3)cn=log2(an+1)=log2(2n-1+1)=log22n=n,(n∈N*),
∴

∴
 =
= =
=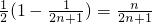
分析:(1)由题意可知数列{bn}是首项b1=2,公比q=2的等比数列.故bn=b1qn-1=2n.
(2)由an+1-an=2n(n∈N*)可知an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,由此能够求出数列{an}的通项公式.
(3)根据题意,可知
 ,由此能够求出答案.
,由此能够求出答案.点评:本题考查数列的性质和应用,具有一定的难度,解题时要注意公式的合理选用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目