题目内容
与双曲线 有共同的渐近线,且经过点A(-3,
有共同的渐近线,且经过点A(-3, )的双曲线的一个焦点到一条渐近线的距离是( )
)的双曲线的一个焦点到一条渐近线的距离是( )A.8
B.4
C.2
D.1
【答案】分析:先设双曲线方程为 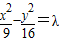 ,再将点
,再将点 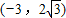 代入双曲线方程,解得λ,从而确定双曲线方程的焦点坐标、渐近线方程,故可利用点到直线距离公式求解.
代入双曲线方程,解得λ,从而确定双曲线方程的焦点坐标、渐近线方程,故可利用点到直线距离公式求解.
解答:解:∵与双曲线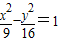 有共同的渐近线,
有共同的渐近线,
∴设双曲线方程为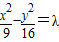 ,
,
将点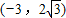 代入双曲线方程,
代入双曲线方程,
解得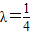 ,⇒
,⇒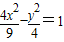
从而所求双曲线方程的焦点坐标为( ,0),一条渐近线方程为
,0),一条渐近线方程为 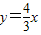 ,
,
所以焦点到一条渐近线的距离是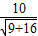 =2,
=2,
故选C.
点评:本题主要考查双曲线的标准方程及几何性质,关键是共渐近线双曲线方程的假设及点到直线距离公式的运用.
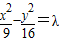 ,再将点
,再将点 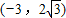 代入双曲线方程,解得λ,从而确定双曲线方程的焦点坐标、渐近线方程,故可利用点到直线距离公式求解.
代入双曲线方程,解得λ,从而确定双曲线方程的焦点坐标、渐近线方程,故可利用点到直线距离公式求解.解答:解:∵与双曲线
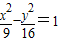 有共同的渐近线,
有共同的渐近线,∴设双曲线方程为
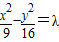 ,
,将点
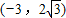 代入双曲线方程,
代入双曲线方程,解得
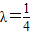 ,⇒
,⇒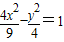
从而所求双曲线方程的焦点坐标为(
 ,0),一条渐近线方程为
,0),一条渐近线方程为 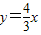 ,
,所以焦点到一条渐近线的距离是
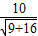 =2,
=2,故选C.
点评:本题主要考查双曲线的标准方程及几何性质,关键是共渐近线双曲线方程的假设及点到直线距离公式的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有共同的渐近线,且过点(2, 2)的双曲线方程为
有共同的渐近线,且过点(2, 2)的双曲线方程为 B.
B.
 D.
D.
 有共同的渐近线,且过点M(2,-2)的双曲线方程为 .
有共同的渐近线,且过点M(2,-2)的双曲线方程为 .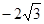 ,1),Q(
,1),Q(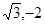 )的椭圆的标准方程.
)的椭圆的标准方程.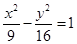 有共同的渐近线,且经过点
有共同的渐近线,且经过点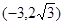 的双曲线的标准方程.
的双曲线的标准方程.
 有共同的渐近线,并且经过点
有共同的渐近线,并且经过点 的双曲线方程.
的双曲线方程. 有共同的渐近线,且经过点P(1,4)的双曲线方程为 ( )
有共同的渐近线,且经过点P(1,4)的双曲线方程为 ( ) B.
B. C.
C. D.
D.