题目内容
在平面直角坐标系中,A={(x,y)|x+ty<2,且t∈R,x≥0,y≥0},若平面区域B={(m,n)|(m-n,m+n)∈A}的面积小于1,则t的取值范围为分析:由于(m-n,m+n)∈A,得出关于m,n的约束条件,在mon系中作出其表示的平面区域,如图,其中三角形OAB的面积为1,欲使得平面区域B={(m,n)|(m-n,m+n)∈A}的面积小于1,则直线(1+t)m+(t-1)n=2的斜率
<-1,从而即可求得t的取值范围.
| 1+t |
| 1-t |
解答: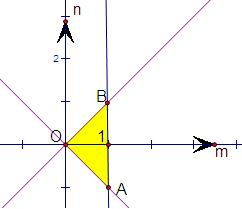 解析:由于(m-n,m+n)∈A,
解析:由于(m-n,m+n)∈A,
∴
在mon系中作出其表示的平面区域,如图,
其中三角形OAB的面积为1,
若平面区域B={(m,n)|(m-n,m+n)∈A}的面积小于1,则直线(m-n)x+t(m+n)=2,
即(1+t)m+(t-1)n=2的斜率
<-1,
解得t>1.
则t的取值范围为t>1.
故答案为:t>1.
 解析:由于(m-n,m+n)∈A,
解析:由于(m-n,m+n)∈A,∴
|
在mon系中作出其表示的平面区域,如图,
其中三角形OAB的面积为1,
若平面区域B={(m,n)|(m-n,m+n)∈A}的面积小于1,则直线(m-n)x+t(m+n)=2,
即(1+t)m+(t-1)n=2的斜率
| 1+t |
| 1-t |
解得t>1.
则t的取值范围为t>1.
故答案为:t>1.
点评:本题主要考查了二元一次不等式(组)与平面区域,解答关键是求出点满足的约束条件,画出不等式组表示的平面区域,求出图象的面积.线性规划主要考查转化能力,与其他知识的结合重点在于问题的转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目