Question

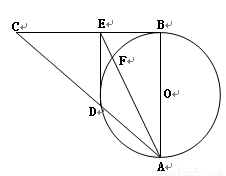
如图在Rt△ABC中，三个顶点坐标分别为A（-1，0），B（1，0），，曲线E过C点且曲线E上任一点P满足|PA|+|PB|是定值．
（Ⅰ）求出曲线E的标准方程；
（Ⅱ）设曲线E与x轴，y轴的交点分别为D、Q，是否存在斜率为k的直线l过定点与曲线E交于不同的两点M、N，且向量与共线．若存在，求出此直线方程；若不存在，请说明理由．

Answer 1

【答案】分析：（Ⅰ）利用题设点P满足|PA|+|PB|是定值，可知点P的及轨迹是以A，B为焦点的椭圆，从而可求曲线E的标准方程；（Ⅱ）设l方程与椭圆方程联立，利用l与椭圆有2个不同交点确定k的取值范围，利用向量与共线，求出k的取值，由此即可得到结论．
解答：解：（Ⅰ）由题设，|AC|=，|AB|=2，|BC|=
∵点P满足|PA|+|PB|是定值．
∴|PA|+|PB|=+=2＞|AB|
由椭圆的定义，可知点P的轨迹是以A，B为焦点的椭圆，且a=，c=1，b=
∴曲线E的标准方程为；
（Ⅱ）由已知条件l方程为y=kx+，由消去y整理得（1+2k²）x²+x+2=0
l与椭圆有2个不同交点的条件为△=32k²-8（1+2k²）＞0，解得或
若l与椭圆交于M（x₁，y₁），N（x₂，y₂），∴，
=（x₁+x₂，y₁+y₂）
椭圆与x轴，y轴交点D（，0），Q（0，1），
∵向量与共线
∴
∴
解得k=∉
∴不存在符合题设条件的直线l．
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查向量知识的运用，直线与椭圆联立，利用韦达定理是解题的关键．