题目内容

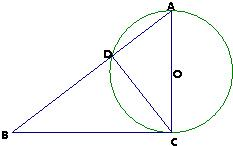
如图所示，以直角三角形ABC的直角边AC为直径作⊙O，交斜边AB于点D，过点D作⊙O的切线，交BC边于点E．则 $数学公式$ =________．

$\text{[math]}$
分析：连接CD，由AC是⊙O的直径，可得CD⊥AB．可证BC是⊙O的切线，及DE是⊙O的切线，由切线长定理可得ED=EC，在Rt△BCD可证明点E是斜边的中点，即可得出结论．
解答：连接CD，∵AC是⊙O的直径，∴CD⊥AB．
∵BC经过半径OC的端点C且BC⊥AC，∴BC是⊙O的切线，
而DE是⊙O的切线，∴EC=ED．
∴∠ECD=∠CDE，∴∠B=∠BDE，∴DE=BE．
∴BE=CE= $\text{[math]}$ BC．
∴ $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：熟练掌握圆的性质、切线长定理、直角三角形的边角关系数据他的关键．