题目内容
 如图所示,已知直角三角ACB中,BC=4,AC=3,以AC为直径作圆O交于D,则DC=________.
如图所示,已知直角三角ACB中,BC=4,AC=3,以AC为直径作圆O交于D,则DC=________.

分析:综合题设中的条件与图形,CD是直角三角形BCA斜边上的高,由于此直角三角形的三边长度可求,故可以用等面积法建立起起关于CD的方程,求之.
解答:∠ADC为直径AC所对的圆周角,则∠ADC=90°,在Rt△ACB中,CD⊥AB,
又直角三角ACB中,BC=4,AC=3,可得AB=5
由等面积法有AB•CD=CA•CB,即5×CD=3×4
故得
 .
.故答案为:

点评:本题考点是与圆有关的成比例线段,由于本题图形特殊,故求此线段长度的方法用等面积法即可,在平面几何中利用面积相等求线段的长度是一个利器,应好好把握次方法运用的条件:面积易求,所对的边易求,此线段恰好是高.

练习册系列答案
相关题目
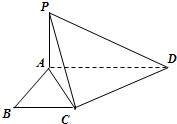 如图所示,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD.
如图所示,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD.
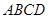 是直角梯形,
是直角梯形,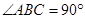 ,
,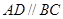 ,
,
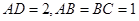 ,
,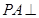 平面
平面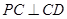 ;
; 是
是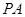 的中点,证明:
的中点,证明: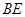 ∥平面
∥平面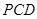 ;
;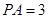 ,求三棱锥
,求三棱锥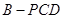 的体积.
的体积. ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
, ,其中
,其中 、
、

 ,求直线
,求直线 与平面
与平面 所成角的大小。
所成角的大小。