题目内容
平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).(1)求3a+b-2c;
(2)求满足a=mb+nc的实数m,n;
(3)若a+kc∥(2b-a),求实数k;
(4)设d=(x,y)满足(d-c)∥(a+b)且|d-c|=1,求d.
思路分析:对于(1),可直接用坐标运算得出结果.对于(2),可将向量相等转化为关于坐标的方程组.对于(3)(4),都可运用向量平行的条件,将其转化为关于坐标的等式求解.
解:(1)3a+b-2c=3(3,2)+(-1,2)-2(4,1)=(0,6).
(2)∵a=mb+nc,∴(3,2)=m(-1,2)+n(4,1)=(-m+4n,2m+n).
∴
(3)∵(a+kc)∥(2b-a),又a+kc=(3+4k,2+k),2b-a=(-5,2),
∴2×(3+4k)-(-5)×(2+k)=0.
∴k=![]() .
.
(4)∵d-c=(x-4,y-1),a+b=(2,4),
又(d-c)∥(a+b)且|d-c|=1,
∴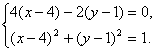
解之,得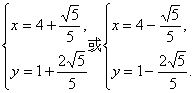
∴d=(![]() )或d=(
)或d=(![]() ).
).

练习册系列答案
相关题目