题目内容
12. 已知,正方形ABCD-A1B1C1D1,E、M、F分别是AD、CD、CC1的中点,
已知,正方形ABCD-A1B1C1D1,E、M、F分别是AD、CD、CC1的中点,求证:(1)EM∥平面BFD1;
(2)A1E⊥平面ABF.
分析 (1)设正方向边长为1,以D为原点,分别以线段DC,DA,DD1的正方向为x,y,z轴,建立空间直角坐标系,则由题意可得:$\overrightarrow{{FD}_{1}}$=(0,-1,$\frac{1}{2}$),$\overrightarrow{FB}$=(1,0,-$\frac{1}{2}$),设平面平面BFD1的法向量为:$\overrightarrow{n}=(x,y,z)$,由$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{{FD}_{1}}=0\\ \overrightarrow{n}•\overrightarrow{FB}=0\end{array}\right.$,不妨令z=2,则$\overrightarrow{n}$=(1,1,2).由$\overrightarrow{ME}•\overrightarrow{n}$=0,即可证明EM∥平面BFD1;
(2)由题意可得坐标$\overrightarrow{{A}_{1}E}$=(0,-$\frac{1}{2}$,-1),$\overrightarrow{BF}$=(0,-1,$\frac{1}{2}$),由于:$\overrightarrow{{A}_{1}E}$•$\overrightarrow{BF}$=0,可证A1E⊥BF,又AB⊥A1E,即可证明A1E⊥平面ABF.
解答 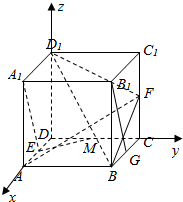 证明:(1)如图,设正方向边长为1,以D为原点,分别以线段DC,DA,DD1的正方向为x,y,z轴,建立空间直角坐标系,
证明:(1)如图,设正方向边长为1,以D为原点,分别以线段DC,DA,DD1的正方向为x,y,z轴,建立空间直角坐标系,
则由题意可得:D(0,0,0),E(0,$\frac{1}{2}$,0),D1(0,0,1),B(1,1,0),F(0,1,$\frac{1}{2}$),$\overrightarrow{{FD}_{1}}$=(0,-1,$\frac{1}{2}$),$\overrightarrow{FB}$=(1,0,-$\frac{1}{2}$),
设平面平面BFD1的法向量为:$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{{FD}_{1}}=0\\ \overrightarrow{n}•\overrightarrow{FB}=0\end{array}\right.$,可得$\left\{\begin{array}{l}-y+\frac{1}{2}z=0\\ x-\frac{1}{2}z=0\end{array}\right.$,不妨令z=2,则$\overrightarrow{n}$=(1,1,2).
$\overrightarrow{ME}$=($\frac{1}{2}$,-$\frac{1}{2}$,0).
$\overrightarrow{ME}•\overrightarrow{n}$=0,ME?平面BFD1;
∴EM∥平面BFD1;
(2)由题意可得:D(0,0,0),E(0,$\frac{1}{2}$,0),A1(1,0,1),B(1,1,0),F(0,1,$\frac{1}{2}$),
可得:$\overrightarrow{{A}_{1}E}$=(0,-$\frac{1}{2}$,-1),$\overrightarrow{BF}$=(0,-1,$\frac{1}{2}$),
由于:$\overrightarrow{{A}_{1}E}$•$\overrightarrow{BF}$=0+$\frac{1}{2}$$-\frac{1}{2}$=0,
所以:A1E⊥BF,
又∵正方形ABCD-A1B1C1D1中,AB⊥A1E,AB∩BF=B,
∴A1E⊥平面ABF.
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和推理论证能力,考查了空间直角坐标系的应用,属于中档题.

| A. | $1-\sqrt{3}$ | B. | $1+\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $1+\sqrt{3}$ |
| A. | a>b>0是1a<1b的充要条件 | |
| B. | 若a+b+c=0,则a>b>c是ac<0的充分而不必要条件 | |
| C. | ac2>bc2是a>b的必要而不充分条件 | |
| D. | a>b且c>d是a-c>b-d的必要不充分条件 |
| A. | 5$\sqrt{2}$ | B. | 8 | C. | 6$\sqrt{3}$ | D. | 12 |
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |