题目内容
函数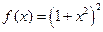 的极值情况是: 极大值; 极小值(填“存在”或“不存在”)。
的极值情况是: 极大值; 极小值(填“存在”或“不存在”)。
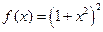 的极值情况是: 极大值; 极小值(填“存在”或“不存在”)。
的极值情况是: 极大值; 极小值(填“存在”或“不存在”)。只有极小值,不存在极大值
 ,∴
,∴ ,∴
,∴ 在
在 上为增函数,在
上为增函数,在 上为减函数,∴只有极小值,不存在极大值。
上为减函数,∴只有极小值,不存在极大值。
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
题目内容
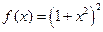 的极值情况是: 极大值; 极小值(填“存在”或“不存在”)。
的极值情况是: 极大值; 极小值(填“存在”或“不存在”)。 ,∴
,∴ ,∴
,∴ 在
在 上为增函数,在
上为增函数,在 上为减函数,∴只有极小值,不存在极大值。
上为减函数,∴只有极小值,不存在极大值。
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案