题目内容
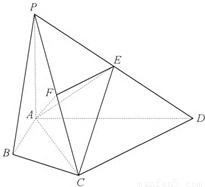
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.(1)求四棱锥P-ABCD的体积V;
(2)若F为PC的中点,求证PC⊥平面AEF;
(3)求证CE∥平面PAB.
【答案】分析:(1)利用直角三角形中的边角关系求出BC、AC、CD,由 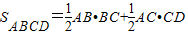 求得底面的面积,
求得底面的面积,
代入体积公式进行运算.
(2)证明AF⊥PC,再由CD⊥平面PAC 证明CD⊥PC,由EF∥CD,可得PC⊥EF,从而得到PC⊥平面AEF.
(3)延长DC,AB,设它们交于点N,证明EC是三角形DPN的中位线,可得EC∥PN,从而证明EC∥平面PAB.
解答:解:(1)在Rt△ABC中,AB=1,∠BAC=60°,∴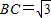 ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠ACD=60°,∴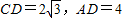 .
.
∴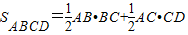 =
=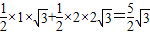 .
.
则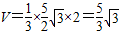 .
.
(2)证明:∵PA=CA,F为PC的中点,∴AF⊥PC.
∵PA⊥平面ABCD,∴PA⊥CD,∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC,∴CD⊥PC.
∵E为PD中点,F为PC中点,∴EF∥CD,则EF⊥PC,∵AF∩EF=F,∴PC⊥平面AEF.
(3)证明:延长DC,AB,设它们交于点N,连PN.∵∠NAC=∠DAC=60°,AC⊥CD,
∴C为ND的中点.∵E为PD中点,∴EC∥PN.∵EC?平面PAB,PN?平面PAB,
∴EC∥平面PAB.
点评:本题考查证明线线垂直、线面垂直的方法,求棱锥的体积,证明CE∥平面PAB 是解题的难点.
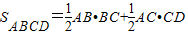 求得底面的面积,
求得底面的面积,代入体积公式进行运算.
(2)证明AF⊥PC,再由CD⊥平面PAC 证明CD⊥PC,由EF∥CD,可得PC⊥EF,从而得到PC⊥平面AEF.
(3)延长DC,AB,设它们交于点N,证明EC是三角形DPN的中位线,可得EC∥PN,从而证明EC∥平面PAB.
解答:解:(1)在Rt△ABC中,AB=1,∠BAC=60°,∴
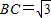 ,AC=2.
,AC=2.在Rt△ACD中,AC=2,∠ACD=60°,∴
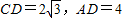 .
.∴
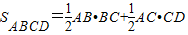 =
=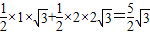 .
.则
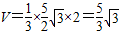 .
.(2)证明:∵PA=CA,F为PC的中点,∴AF⊥PC.
∵PA⊥平面ABCD,∴PA⊥CD,∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC,∴CD⊥PC.
∵E为PD中点,F为PC中点,∴EF∥CD,则EF⊥PC,∵AF∩EF=F,∴PC⊥平面AEF.
(3)证明:延长DC,AB,设它们交于点N,连PN.∵∠NAC=∠DAC=60°,AC⊥CD,
∴C为ND的中点.∵E为PD中点,∴EC∥PN.∵EC?平面PAB,PN?平面PAB,
∴EC∥平面PAB.
点评:本题考查证明线线垂直、线面垂直的方法,求棱锥的体积,证明CE∥平面PAB 是解题的难点.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,