题目内容
(理科)若对于一切正实数x不等式| 4+2x2 | x |
分析:由题意得:对于一切正实数x不等式
>a恒成立,由于
=
+2x的最小值等于4
,可得a小于其最小值即可,从而求得答案.
| 4+2x2 |
| x |
| 4+2x2 |
| x |
| 4 |
| x |
| 2 |
解答:解:∵对于一切正实数x不等式
>a恒成立
由于
=
+2x≥2
=4
,
∴
的最小值等于4
,可得a小于其最小值4
即可,
∴a<4
,
故答案为 a<4
.
| 4+2x2 |
| x |
由于
| 4+2x2 |
| x |
| 4 |
| x |
|
| 2 |
∴
| 4+2x2 |
| x |
| 2 |
| 2 |
∴a<4
| 2 |
故答案为 a<4
| 2 |
点评:本题考查查绝对值不等式的解法,基本不等式的应用以及函数的恒成立问题,求出
的最小值等于是解题的关键.
| 4+2x2 |
| x |

练习册系列答案
相关题目
 >a恒成立,则实数a的取值范围是 .
>a恒成立,则实数a的取值范围是 .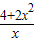 >a恒成立,则实数a的取值范围是 .
>a恒成立,则实数a的取值范围是 .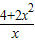 >a恒成立,则实数a的取值范围是 .
>a恒成立,则实数a的取值范围是 .