题目内容
设椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交与两不同点
相交与两不同点![]() 时,在线段
时,在线段![]() 上取点
上取点![]() ,满足
,满足 =
=![]() ,证明:点
,证明:点![]() 的轨迹与
的轨迹与![]() 无关.
无关.
解(Ⅰ)由题意解得![]() ,所求椭圆方程为
,所求椭圆方程为 ![]() .…………4分
.…………4分
(Ⅱ)方法一
设点Q、A、B的坐标分别为![]() .
.
由题设 ,
,![]() 则
则![]() 且
且![]() .
.

(1)+(2)×2并结合(3),(4)得![]() ,…………14分
,…………14分
点![]() 总在定直线
总在定直线![]() 上.即点
上.即点![]() 的轨迹与
的轨迹与![]() 无关.…………15分
无关.…………15分
方法二
设点![]() ,由题设
,由题设  =
=![]() .
.
又 ![]() 四点共线,可得
四点共线,可得![]() ,…………6分
,…………6分
于是
![]() (1)
(1)
![]() (2)
(2)
由于![]() 在椭圆C上,将(1),(2)分别代入C的方程
在椭圆C上,将(1),(2)分别代入C的方程![]() 整理得
整理得
![]() (3)
(3)
![]() (4)
(4)
…………10分
(4)-(3) 得 ![]() ,
,
![]() ,…………14分
,…………14分
点![]() 总在定直线
总在定直线![]()
![]() 上.即点
上.即点![]() 的轨迹与
的轨迹与![]() 无关.…………15分
无关.…………15分

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 过点
过点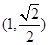 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线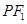 和
和 与椭圆的交点分别为
与椭圆的交点分别为 、
、 和
和 、
、 ,
, 为坐标原点.设直线
为坐标原点.设直线 、
、 .
.
 ;
; 上是否存在点
上是否存在点 、
、 、
、 、
、 的斜率
的斜率 、
、 、
、 、
、 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 过点.
过点. ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为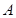 、
、 和
和 、
、 ,
, 为坐标原点.
为坐标原点. 、
、 . 证明:
. 证明:

 过点
过点 ,离心率为
,离心率为 ,左、右焦点分别为F1、F2。点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点。
,左、右焦点分别为F1、F2。点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点。
 ;
;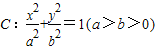 过点
过点 ,离心率为
,离心率为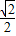 .
.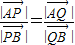 =λ,证明:点Q的轨迹与λ无关.
=λ,证明:点Q的轨迹与λ无关.