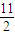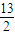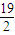Question

已知方程（x²-4x-m）（x²-4x-n）=0的四个实根组成以

1

2

为首项的等差数列，则|m+n|=（　　）

• A、2
• B、

  11

  2

• C、

  13

  2

• D、

  19

  2

Answer 1

分析：若设a，b，c，d分别是方程：x²-4x-m=0和x²-4x-n=0的实数根，则a+b=c+d=4；不妨设a＜c＜d＜b，则a=

1

2

，b=

7

2

；根据等差数列的性质，可得c=

3

2

，d=

5

2

；由根与系数的关系，得-m=ab，-n=cd；从而求出|m+n|的值．

解答：解：根据题意，设a，b，c，d分别是方程：x²-4x-m=0和x²-4x-n=0的实数根，由根与系数的关系，得
a+b=c+d=4，不妨假设a＜c＜d＜b，则a=

1

2

，b=

7

2

；
由a，b，c，d成等差数列，得：c=

3

2

，d=

5

2

； 所以，-m=ab=

7

4

，-n=cd=

15

4

，即m=-

7

4

，n=-

15

4

；
所以，|m+n|=

11

2

．

点评：本题考查了等差数列与一元二次方程根与系数的综合应用，解题时要认真分析，灵活运用所学的知识，解出结果．