题目内容
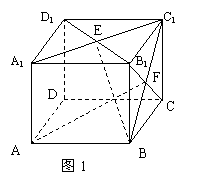
（14分）.如图1，在长方体AC1中，AB=BC=2，AA1=
，E、F分别是A1C1.、BC1的中点。
求 (1) AF和BE所成的角.
(2) AA1与平面BEC1所成的角.
（1）
（2）450
|
解：（1）以D为原点，以DA,DC,DD1为x,y,z轴，建立如图所示的直角坐标系，则A(2,0,0) B(2, 2,0) C(0,2,0) A1（2，0，
）B1(2,2,) C1(0,2, ) D1（0，0，）
|
因为E，F分别是B1D和B1C的中点，所以E(1,1, ) F(1,2, 
),所以
，
，
，
，所以AF和BE所成的角为900 …………………………7分 （2）
，
，
设平面BEC1的法向量为
，则
，
，
，
，令y=1,x=1,z=,
设AA1与平面BEC1所成的角为θ，则
sinθ=
,所以θ=450……………………………………14分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图1在透明塑料做成的长方体容器中灌进一些水，固定容器的一边将其倾倒，随着容器的倾斜度不同，水的各个表面的图形的形状和大小也不同．某个同学找出这些图形的形状和大小之间所存在的一些“规律”：①有水的部分始终呈棱柱形；②没有水的部分始终呈棱柱形；③水面面积的大小是变化的，如图2所示，倾斜度越大（即α越小），水面的面积越大．④如果长方体的倾斜角为α，则水面与容器底面所成的角为90°-α．
