题目内容
7.函数y=1+2cos (3+4x)的最小正周期是$\frac{π}{2}$.分析 由条件利用y=Asin(ωx+φ)+k 的周期等于 T=$\frac{2π}{ω}$,得出结论.
解答 解:函数y=1+2cos (3+4x)的最小正周期为 $\frac{2π}{4}$=$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题主要考查三角函数的周期性及其求法,利用了y=Asin(ωx+φ)+k的周期等于 T=$\frac{2π}{ω}$,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
12.已知tanx=$\frac{1}{3}$,则sin2x=( )
| A. | $\frac{\sqrt{3}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
16.已知函数f(x)=ln(1+x2),则满足不等式f(2x-1)<f(3)的x的取值范围是( )
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |
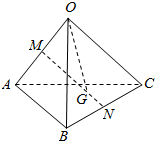 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.