题目内容
设a,b,c∈R且abc≠0,则由代数式
+
+
+
的值组成的集合为______.(用列举法表示)
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
当a,b,c中,有两个大于0,一个小于0,
+
+
+
=1+1-1-1=0;
当a,b,c中,有两个小于0,一个大于0时,
+
+
+
=1+1-1-1=0;
当a,b,c都小于0时,
+
+
+
=-1-1-1-1=-4;
当a,b,c都大于0时,
+
+
+
=1+1+1+1=4.
所以由代数式
+
+
+
的值组成的集合为{-4,0,4}.
故答案为:{-4,0,4}.
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
当a,b,c中,有两个小于0,一个大于0时,
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
当a,b,c都小于0时,
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
当a,b,c都大于0时,
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
所以由代数式
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
故答案为:{-4,0,4}.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
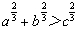 .
. .
.