Question

【题目】已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ ）的部分图象如图所示．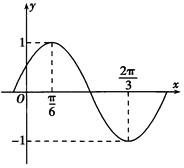
（1）求函数f（x）的解析式，并写出f（x）的单调减区间；
（2）已知△ABC的内角分别是A，B，C，A为锐角，且f（ ﹣ ）= ，求cosA的值．

Answer 1

【答案】
（1）解：由函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ ）的部分图象，可得 = ，∴ω=2，

再根据五点法作图可得2 +φ= ，∴φ= ，f（x）=sin（2x+ ）

（2）解：∵已知△ABC的内角分别是A，B，C，A为锐角，且f（ ﹣ ）=sinA= ，∴A= ，

∴cosA= =

【解析】（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．（2）利用同角三角函数的基本关系，求得 cosA 的值．