题目内容
用数学归纳法证明n为正偶数时xn-yn能被x+y整除.
证明:①当n=2时,x2-y2=(x+y)(x-y),
即x2-y2能被x+y整除,显然命题成立.
②假设n=2k(k∈N*)时,命题成立,即x2k-y2k能被x+y整除.
则当n=2k+2时,x2k+2-y2k+2=x2·x2k-y2·y2k=x2(x2k-y2k)+y2k(x2-y2)
=x2(x2k-y2k)+y2k(x+y)(x-y).
∵x2(x2k-y2k)、y2k(x+y)(x-y)都能被x+y整除,
∴x2k+2-y2k+2能被x+y整除,即n=2k+2时命题成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
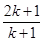 D..
D.. 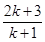
 D..
D.. 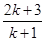
 D.
D.