题目内容
(本小题满分12分)
已知函数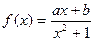 在点
在点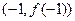 的切线方程为
的切线方程为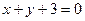
(Ⅰ)求函数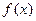 的解析式
的解析式
(Ⅱ)设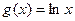 ,求证:
,求证: 在
在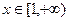 上恒成立
上恒成立
(Ⅲ)已知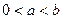 ,求证:
,求证: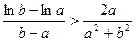
已知函数
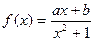 在点
在点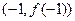 的切线方程为
的切线方程为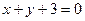
(Ⅰ)求函数
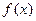 的解析式
的解析式(Ⅱ)设
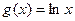 ,求证:
,求证: 在
在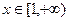 上恒成立
上恒成立(Ⅲ)已知
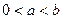 ,求证:
,求证: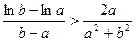
解:(Ⅰ)将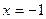 代入切线方程得
代入切线方程得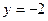
∴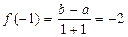 ,化简得
,化简得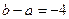 …………………………………………2分
…………………………………………2分
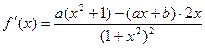
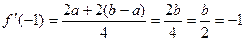
解得: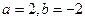 .
.
∴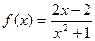 . …………………………………………4分
. …………………………………………4分
(Ⅱ)由已知得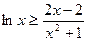 在
在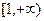 上恒成立
上恒成立
化简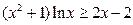
即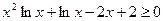 在
在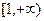 上恒成立
上恒成立
设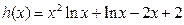 ,
,
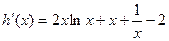
 …………………………………………6分
…………………………………………6分
∵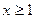 ∴
∴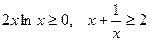 ,即
,即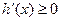
∴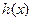 在
在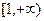 上单调递增,
上单调递增,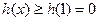
∴ 在
在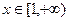 上恒成立 …………………………………………8分
上恒成立 …………………………………………8分
(Ⅲ)∵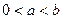 ∴
∴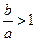 ,
,
由(Ⅱ)知 有
有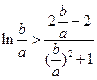 , …………………………………………10分
, …………………………………………10分
整理得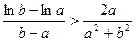
∴当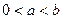 时,
时,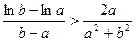 . …………………………………………12分
. …………………………………………12分
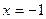 代入切线方程得
代入切线方程得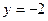
∴
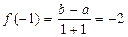 ,化简得
,化简得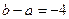 …………………………………………2分
…………………………………………2分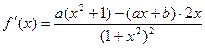
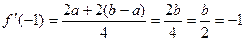
解得:
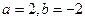 .
.∴
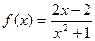 . …………………………………………4分
. …………………………………………4分(Ⅱ)由已知得
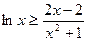 在
在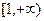 上恒成立
上恒成立化简
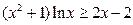
即
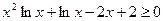 在
在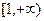 上恒成立
上恒成立设
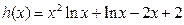 ,
,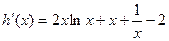
 …………………………………………6分
…………………………………………6分∵
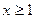 ∴
∴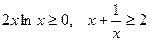 ,即
,即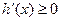
∴
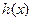 在
在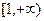 上单调递增,
上单调递增,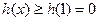
∴
 在
在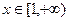 上恒成立 …………………………………………8分
上恒成立 …………………………………………8分(Ⅲ)∵
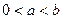 ∴
∴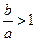 ,
,由(Ⅱ)知
 有
有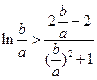 , …………………………………………10分
, …………………………………………10分整理得
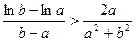
∴当
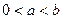 时,
时,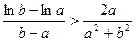 . …………………………………………12分
. …………………………………………12分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
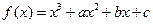 是定义在
是定义在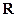 上的奇函数,其图象过点
上的奇函数,其图象过点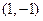 和
和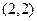 .
.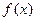 的解析式,并求
的解析式,并求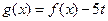 ,当实数
,当实数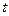 如何取值时,关于
如何取值时,关于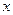 的方程
的方程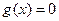 有且只有一个实
有且只有一个实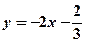 与曲线
与曲线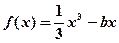 相切
相切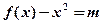 在
在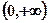 上恰有两个不等的实数根
上恰有两个不等的实数根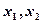 ,求
,求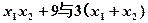 的大小
的大小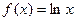
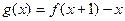 的最大值;
的最大值;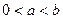 时,求证
时,求证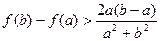 ;
;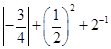 的结果相同的是( ).
的结果相同的是( ).
 )的切线方程
)的切线方程 的极值
的极值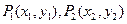 ,如果存在曲线上的点
,如果存在曲线上的点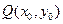 ,且
,且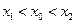 ,使得曲线在点
,使得曲线在点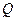 处的切线
处的切线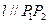 ,则称
,则称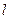 为弦
为弦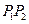 的陪伴切线.已知两点
的陪伴切线.已知两点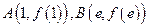 ,试求弦
,试求弦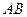 的陪伴切线
的陪伴切线 的导数
的导数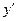 =__________________.
=__________________.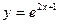 与
与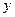 轴的交点的切线方程为_______________。
轴的交点的切线方程为_______________。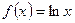 ,若直线
,若直线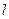 与
与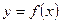 的图象相切的切点的横坐标为1,那么直线
的图象相切的切点的横坐标为1,那么直线