题目内容

设函数y=f(x),且lg(lgy)=lg(3x)+lg(3－x),

(1)求f(x)的表达式及定义域；

(2)求f(x)的值域.

解:(1)若lg(lgy)=lg(3x)+lg(3－x)有意义，

则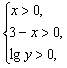即

又∵lg(lgy)=lg(3x)+lg(3－x),

∴lgy=3x(3－x).

∴y=10(0＜x＜3).

(2)∵3x(3－x)=－3x2+9x=－3(x－)2+(0＜x＜3),

∴0＜－3x2+9x≤.∴1＜y≤10.

∴y=f(x)的定义域为(0，3)，值域为(1,10］.

练习册系列答案
相关题目
设函数y=f(x)=ax+
1x+b
(a≠0)的图象过点（0，-1）且与直线y=-1有且只有一个公共点；设点P（x0，y0）是函数y=f（x）图象上任意一点，过点P分别作直线y=x和直线x=1的垂线，垂足分别是M，N．
（1）求y=f（x）的解析式；
（2）证明：曲线y=f（x）的图象是一个中心对称图形，并求其对称中心Q；
（3）证明：线段PM，PN长度的乘积PM•PN为定值；并用点P横坐标x0表示四边形QMPN的面积．．
设函数y=f(x)=
2x
2x+
2
上两点p1（x1，y1），p2（x2，y2），若
op
=
1
2
(
op1
+
op2
)，且P点的横坐标为
1
2
．
（1）求P点的纵坐标；
（2）若Sn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)+f(
n
n
)，求Sn；
（3）记Tn为数列{
1
(Sn+
2
)(Sn+1+
2
)
}的前n项和，若Tn＜a(Sn+2+
2
)对一切n∈N*都成立，试求a的取值范围．
设函数y=f(x)在R上连续,则f(x)在R上为递增函数是f′(x)＞0的…(    )

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

设函数y=f(x)是一次函数,若f(1)=-1,且f′(2)=-4,则f(x)的解析式为_________.

设函数y=f(x)的图象如图所示，则导函数y=f ¢(x)可能为（    ）

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网