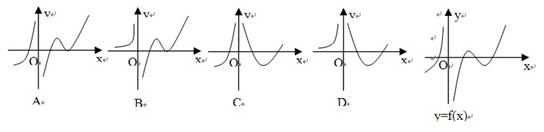
题目内容
设函数y=f(x)=
上两点p1(x1,y1),p2(x2,y2),若
=
(
+
),且P点的横坐标为
.
(1)求P点的纵坐标;
(2)若Sn=f(
)+f(
)+…+f(
)+f(
),求Sn;
(3)记Tn为数列{
}的前n项和,若Tn<a(Sn+2+
)对一切n∈N*都成立,试求a的取值范围.
| 2x | ||
2x+
|
| op |
| 1 |
| 2 |
| op1 |
| op2 |
| 1 |
| 2 |
(1)求P点的纵坐标;
(2)若Sn=f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
(3)记Tn为数列{
| 1 | ||||
(Sn+
|
| 2 |
分析:(1)利用向量知识,确定P为P1P2的中点,即可求得结论;
(2)利用倒序相加法,即可求得结论;
(3)裂项求和,再分离参数,利用基本不等式求最值,即可得到结论.
(2)利用倒序相加法,即可求得结论;
(3)裂项求和,再分离参数,利用基本不等式求最值,即可得到结论.
解答:解:(1)∵
=
(
+
),∴P为P1P2的中点,∴x1+x2=1
∴y1+y2=
+
=1
∴P的纵坐标为
;
(2)由(1)知,x1+x2=1,y1+y2=1,f(1)=2-
∵Sn=f(
)+f(
)+…+f(
)+f(
),Sn=f(
)+f(
)+…+f(
)+f(
)
∴2Sn=(n-1)+2(2-
)=n+3-2
∴Sn=
;
(3)Sn+
=
,Sn+1+
=
∴
=
=4(
-
)
∴Tn=4(
-
+
-
+…+
-
)=
∵Tn<a(Sn+2+
)对一切n∈N*都成立
∴a>
=
设g(n)=n+
,则g(n)在[
,+∞)上是增函数,在(0,
)上是减函数
∴g(n)的最小值为9
∴
<
∴a>
.
| OP |
| 1 |
| 2 |
| OP1 |
| OP2 |
∴y1+y2=
| 2x1 | ||
2x1+
|
| 2x2 | ||
2x2+
|
∴P的纵坐标为
| 1 |
| 2 |
(2)由(1)知,x1+x2=1,y1+y2=1,f(1)=2-
| 2 |
∵Sn=f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| n |
| n |
| n-1 |
| n |
| 2 |
| n |
| 1 |
| n |
∴2Sn=(n-1)+2(2-
| 2 |
| 2 |
∴Sn=
n+3-2
| ||
| 2 |
(3)Sn+
| 2 |
| n+3 |
| 2 |
| 2 |
| n+4 |
| 2 |
∴
| 1 | ||||
(Sn+
|
| 4 |
| (n+3)(n+4) |
| 1 |
| n+3 |
| 1 |
| n+4 |
∴Tn=4(
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+3 |
| 1 |
| n+4 |
| n |
| n+4 |
∵Tn<a(Sn+2+
| 2 |
∴a>
| Tn | ||
Sn+2+
|
| 2 | ||
n+
|
设g(n)=n+
| 20 |
| n |
| 20 |
| 20 |
∴g(n)的最小值为9
∴
| 2 | ||
n+
|
| 1 |
| 9 |
∴a>
| 1 |
| 9 |
点评:本题考查数列的求和,考查裂项法的运用,考查恒成立问题,考查学生分析解决问题的能力,属于中档题

练习册系列答案
相关题目