题目内容
设不等式组 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为![]()
(1)求![]() 的值及
的值及![]() 的表达式;(2)记
的表达式;(2)记![]() ,试比较
,试比较![]() 的大小;若对于一切的正整数
的大小;若对于一切的正整数![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() 为数列
为数列![]() 的前
的前![]() 项的和,其中
项的和,其中![]() ,问是否存在正整数
,问是否存在正整数![]() ,使
,使![]() 成立?若存在,求出正整数
成立?若存在,求出正整数![]() ;若不存在,说明理由。
;若不存在,说明理由。
解:⑴ ![]() ------------------2分
------------------2分
当![]() 时,
时,![]() 取值为1,2,3,…,
取值为1,2,3,…,![]() 共有
共有![]() 个格点
个格点
当![]() 时,
时,![]() 取值为1,2,3,…,
取值为1,2,3,…,![]() 共有
共有![]() 个格点
个格点
∴![]() - ------------------4分
- ------------------4分
(2)记![]() ,试比较
,试比较![]() 的大小;若对于一切的正整数
的大小;若对于一切的正整数![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
解:由![]()
则![]()
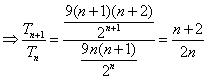
-------------------5分
当![]() 时,
时,![]()
当![]() 时,
时,![]() -------------------6分
-------------------6分
∴![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 时,
时,![]()
∴![]() 中的最大值为
中的最大值为![]() -------------------8分
-------------------8分
要使![]() 对于一切的正整数
对于一切的正整数![]() 恒成立,
恒成立,
只需![]()
∴![]() -------------------9分
-------------------9分
(3)设![]() 为数列
为数列![]() 的前
的前![]() 项的和,其中
项的和,其中![]() ,问是否存在正整数
,问是否存在正整数![]() ,使
,使![]() 成立?若存在,求出正整数
成立?若存在,求出正整数![]() ;若不存在,说明理由。
;若不存在,说明理由。
解:![]() --------------10分
--------------10分
将![]() 代入
代入![]() ,化简得,
,化简得,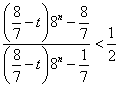 (﹡)-------------------11分
(﹡)-------------------11分
若![]() 时
时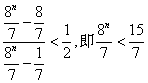 ,显然
,显然![]() -------------------12分
-------------------12分
若![]() 时
时![]() (﹡)式
(﹡)式
化简为![]() 不可能成立-------------------13分
不可能成立-------------------13分
综上,存在正整数![]() 使
使![]() 成立. - --------------14分
成立. - --------------14分

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 所表示的平面区域内的概率.
所表示的平面区域内的概率.