Question

如图,在棱长为1的正方体ABCD—A′B′C′D′中,AP=BQ=b(0＜b＜1),截面PQEF∥A′D,截面PQGH∥AD′.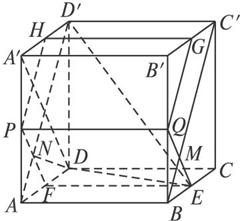

(1)证明平面PQEF和平面PQGH互相垂直;

(2)证明截面PQEF和截面PQGH面积之和是定值,并求出这个值;

(3)若b=,求D′E与平面PQEF所成角的正弦值.

Answer 1

答案：本题主要考查空间中的线面关系、面面关系、解三角形等基础知识,考查空间想象能力与逻辑思维能力.

解法一:(1)证明:在正方体中,AD′⊥A′D,AD′⊥AB,

又由已知可得PF∥A′D,PH∥AD′,PQ∥AB,

所以PH⊥PF,PH⊥PQ.

所以PH⊥平面PQEF.

所以平面PQEF和平面PQGH互相垂直.                                       

(2)证明:由(1)知PF=,PH=.

又截面PQEF和截面PQGH都是矩形,且PQ=1,

所以截面PQEF和截面PQGH面积之和是()×PQ=,是定值.       

(3)解:设AD′交PF于点N,连结EN.

因为AD′⊥平面PQEF,

所以∠D′EN为D′E与平面PQEF所成的角.

因为b=,所以P、Q、E、F分别为AA′、BB′、BC、AD的中点.可知D′N=,D′E=.

所以sin∠D′EN=.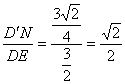                                          

解法二:以D为原点,射线DA、DC、DD′分别为x、y、z轴的正半轴建立如图的空间直角坐标系D—xyz.

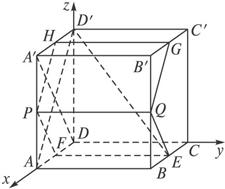
由已知得DF=1-b,故

A(1,0,0),A′(1,0,1),D(0,0,0),D′(0,0,1),P(1,0,b),Q(1,1,b),E(1-b,1,0),F(1-b,0,0),G(b,1,1),B(b,0,1).

(1)证明:在所建立的坐标系中,可得=(0,1,0),=(-b,0,-b), =(b-1,0,1-b), =(-1,0,1),=(-1,0,-1).

因为·=0,·=0,

所以是平面PQEF的法向量.

因为·=0,·=0,

所以是平面PQGH的法向量.

因为·=0,所以⊥.

所以平面PQEF和平面PQGH互相垂直.                                        

(2)证明:因为=(0,-1,0),

所以∥,||=||.

又⊥,所以PQEF为矩形.同理,PQGH为矩形.

在所建立的坐标系中可求得||=(1-b),||=.

所以||+||=.又||=1,

所以截面PQEF和截面PQGH面积之和为,是定值.                           

(3)解:由(1)知=(-1,0,1)是平面PQEF的法向量.

由P为AA′中点可知,Q、E、F分别为BB′、BC、AD的中点.

所以E(,1,0),=(,1,-1),因此D′E与平面PQEF所成角的正弦值等于|cos〈,〉|=.